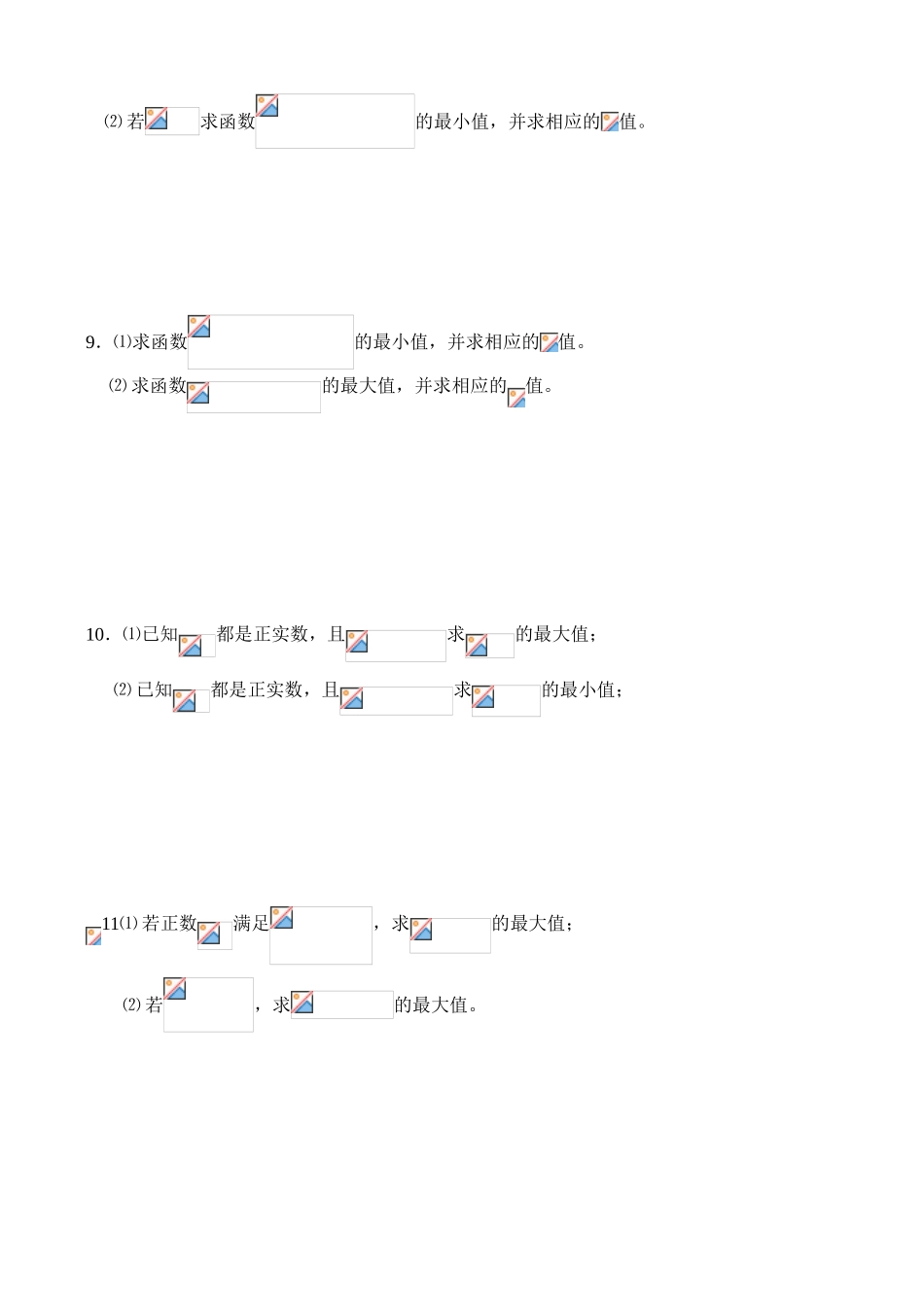
§算术平均数与几何平均数(三) 一.课堂目标:1.掌握极值定理及其相应的适用条件; 2.掌握利用极值定理求最值问题中的变形技巧。二.要点回顾:1.极值定理推广:已知都是正数:⑴ 若是定值,则当时有最小值 ;⑵ 若是定值,则当时,有最大值 。2.定理适用条件:一正二定三相等3.常用变形技巧:拆项要均分,系数可添乘,次数不够可平方。三.目标训练:1.若,则不小于………………………………………………………( )2.已知,且,则的最小值是…………………………………………( )A.4 B. 3.若,且,则的取值范围是…………………( )A. B. C. D.4.若,则的最大值为………………………………………………………( )A. B. C. D. 5.⑴ 函数的最大值是 ,⑵函数的最小值是 。6.⑴函数的最大值是 ,此时 , 。⑵ 函数的最小值是 。8.⑴若求函数的最大值,并求相应的值;浙师大附中课堂目标训练《数学第二册》(上)⑵ 若求函数的最小值,并求相应的值。 9.⑴求函数的最小值,并求相应的值。 ⑵ 求函数的最大值,并求相应的值。10.⑴已知都是正实数,且求的最大值;⑵ 已知都是正实数,且求的最小值;11⑴ 若正数满足,求的最大值;⑵ 若,求的最大值。