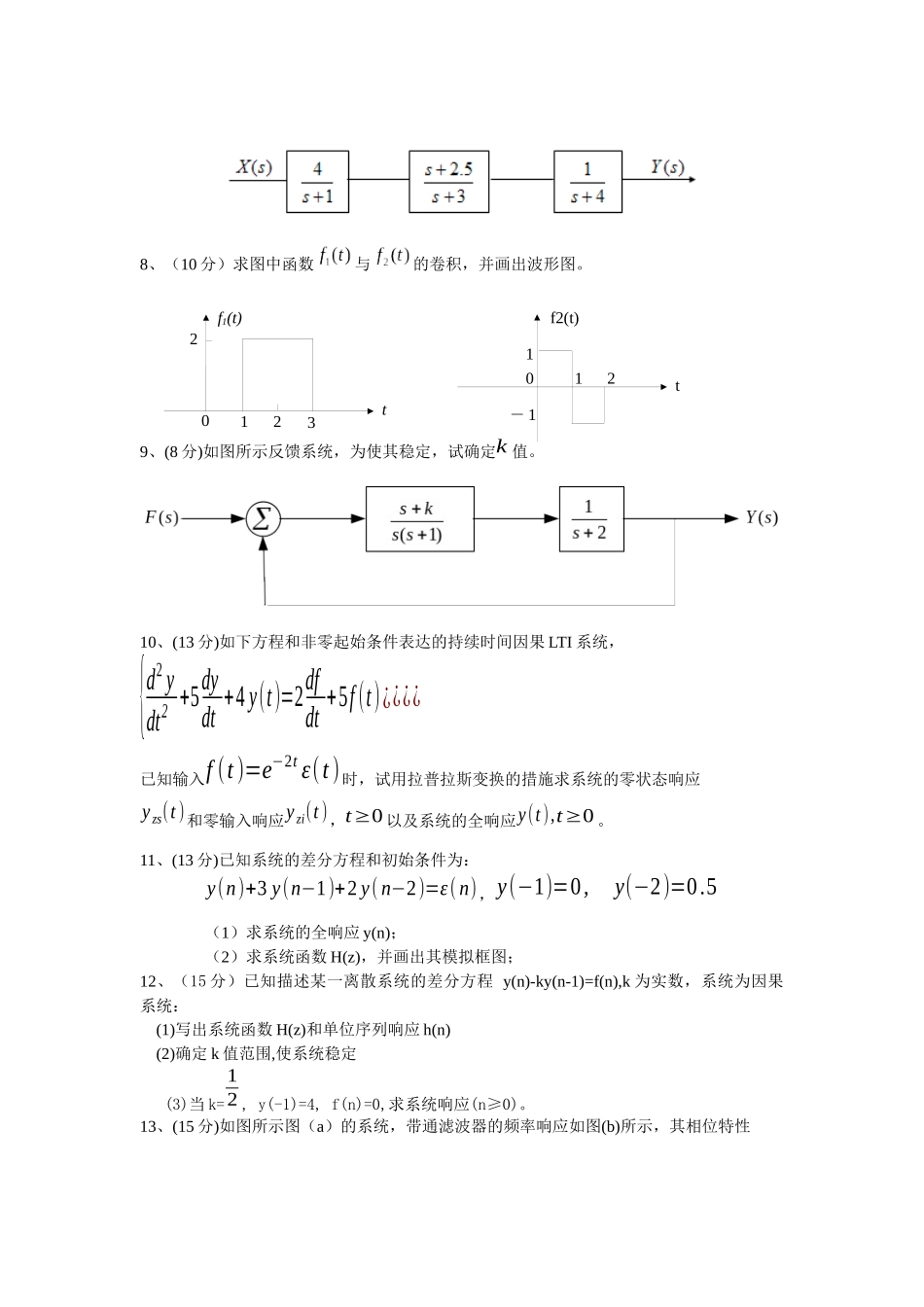
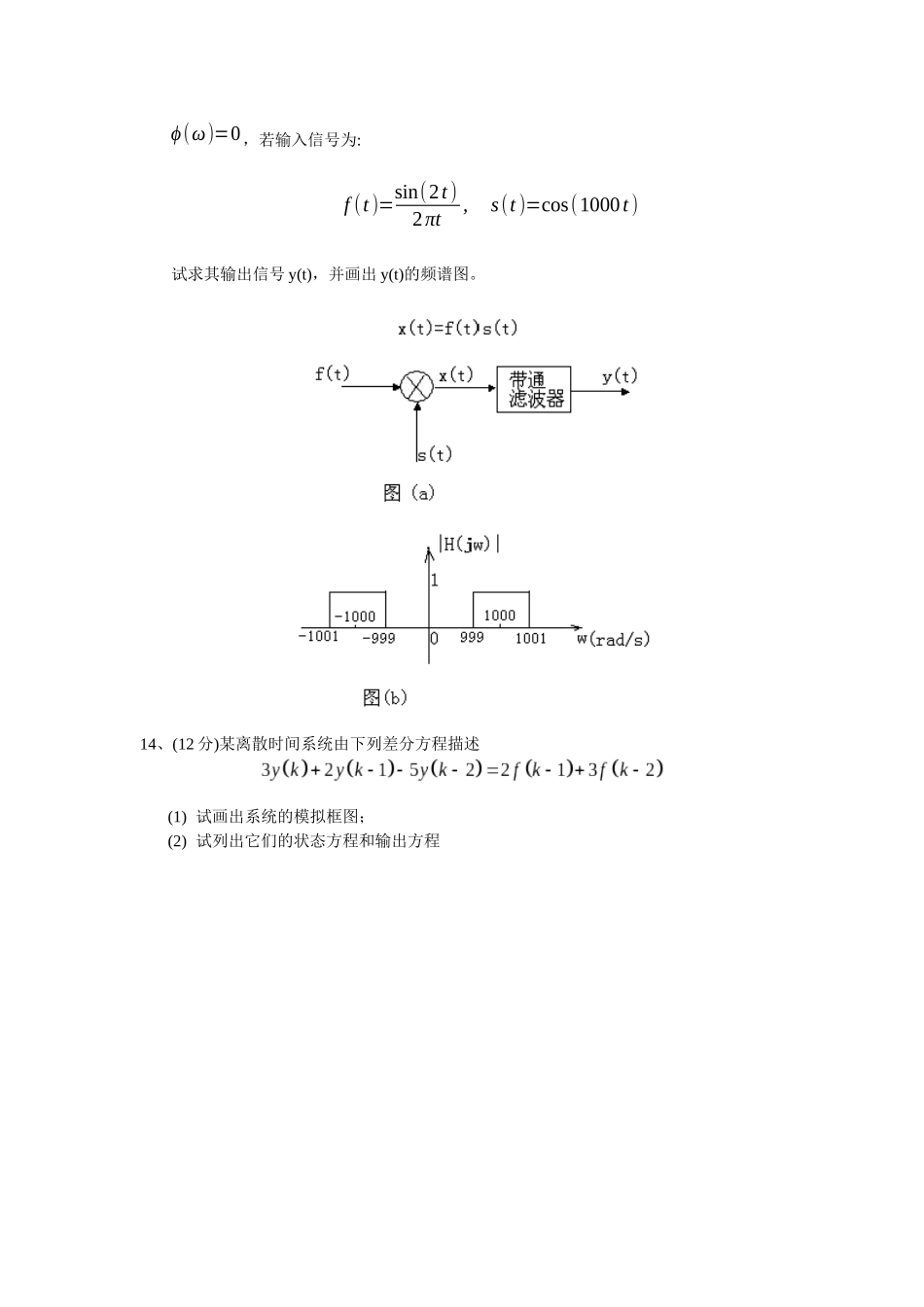
y(n)∑∑Df(n)221/2+++_武汉理工大学硕士入学考试模拟题课程代码: 855 课程名称:信号与系统1、(6 分)求函数F(s)=4( s+1)(s+2)3的拉普拉斯逆变换。2、(6 分)求函数f (t )=sin πt [u(t )−u(t−1)]。3、(10 分)已知x(n)↔ X( z),求下列信号的 z 变换。x1(n)=¿{x(nM) (n=⋯,±M ,±2M ,⋯)¿¿¿¿4、(10 分)已知:X( z )=31−12 z−1+21−2 z−1求出对应X( z )的多种也许的序列体现式。5、(10 分)求如图所示离散系统的单位响应。6、(10 分)已知某系统在作用下全响应为。在作用下全响应为,求阶跃信号作用下的全响应。7、(12 分)如图所示系统的模拟框图(1)写出系统转移函数;(2)当输入为时,求输出。012t1f2(t)- 18、(10 分)求图中函数与的卷积,并画出波形图。9、(8 分)如图所示反馈系统,为使其稳定,试确定k 值。10、(13 分)如下方程和非零起始条件表达的持续时间因果 LTI 系统,{d2 ydt2 +5dydt+4 y(t)=2dfdt+5f (t)¿¿¿¿已知输入f (t )=e−2t ε(t)时,试用拉普拉斯变换的措施求系统的零状态响应y zs(t )和零输入响应y zi(t ),t≥0 以及系统的全响应y(t),t≥0 。11、(13 分)已知系统的差分方程和初始条件为:y(n)+3 y(n−1)+2 y( n−2)=ε( n),y(−1)=0,y(−2)=0.5(1)求系统的全响应 y(n);(2)求系统函数 H(z),并画出其模拟框图;12、(15 分)已知描述某一离散系统的差分方程 y(n)-ky(n-1)=f(n),k 为实数,系统为因果系统: (1)写出系统函数 H(z)和单位序列响应 h(n) (2)确定 k 值范围,使系统稳定 (3)当 k=12 , y(-1)=4, f(n)=0,求系统响应(n≥0)。13、(15 分)如图所示图(a)的系统,带通滤波器的频率响应如图(b)所示,其相位特性01232tf1(t)ϕ(ω)=0,若输入信号为:f (t )=sin(2t )2πt,s(t )=cos(1000t )试求其输出信号 y(t),并画出 y(t)的频谱图。14、(12 分)某离散时间系统由下列差分方程描述(1) 试画出系统的模拟框图;(2) 试列出它们的状态方程和输出方程参照答案(经供参照)1、解:原式展开成部分分式F(s)=4( s+1)(s+2)3 = 4s+1+ −4( s+2)3 + −4(s+2)2 + −4s+2因此 2、解:f (t )=sin π tu(t)+sin π(t−1)u(t−1)F(s)=πs2+π 2+πs2+π 2 e−s= π (1+e−s)s2+π23、解: 因此 X1( z)=X( zM)4、解:X( z )有两个极点:z1=0.5,z2=2,由于收敛域总是以极点为边界,因此收敛域有如下三种状况...