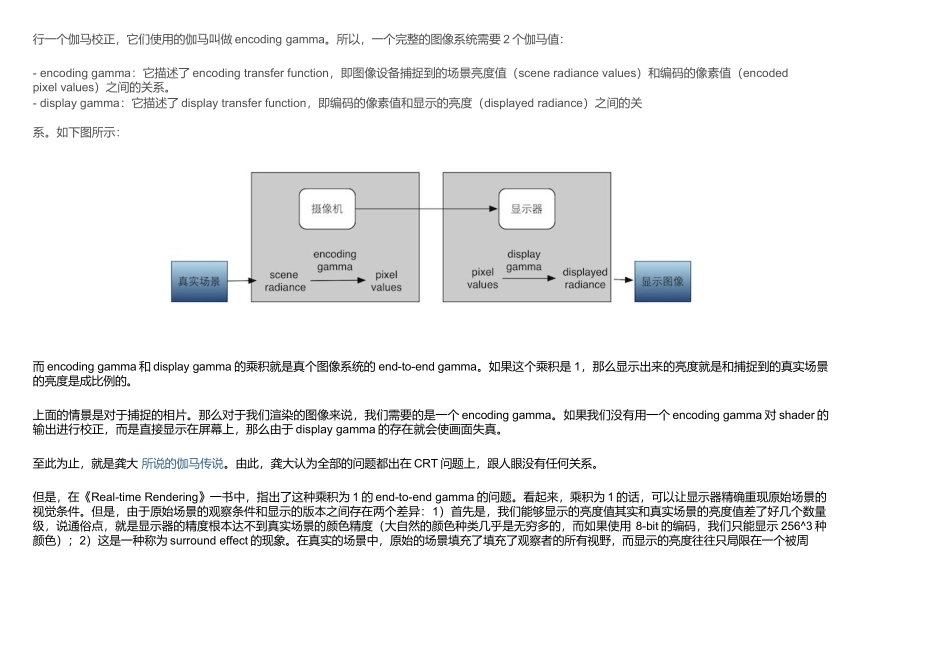
【图形学】我理解的伽马校正(GammaCorrection)写在前面我相信几乎所有做图像处理方面的人都听过伽马校正(GammaCorrection)这一个名词,但真正明白它是什么、为什么要有它、以及怎么用它的人其实不多。我也不例外。最初我查过一些资料,但很多文章的说法都不一样,有些很晦涩难懂。直到我最近在看《RealTimeRendering,3rdEdition》这本书的时候,才开始慢慢对它有所理解。本人才疏学浅,写的这篇文章很可能成为网上另一篇误导你的“伽马传说”,但我尽可能把目前了解的资料和可能存在的疏漏写在这里。如有错误,还望指出。伽马的传说关于这个方面,龚大写过一篇文章,但我认为其中的说法有不准确的地方。从我找到的资料来看,人们使用伽马曲线来进行显示最开始是源于一个巧合:在早期,CRT几乎是唯一的显示设备。但CRR有个特性,它的输入电压和显示出来的亮度关系不是线性的,而是一个类似幂律(pow-law)曲线的关系,而这个关系又恰好跟人眼对光的敏感度是相反的。这个巧合意味着,虽然CRT显示关系是非线性的,但对人类来说感知上很可能是一致的。我来详细地解释一下这个事件:在很久很久以前(其实没多久),全世界都在使用一种叫CRT的显示设备。这类设备的显示机制是,使用一个电压轰击它屏幕上的一种图层,这个图层就可以发亮,我们就可以看到图像了。但是,人们发现,咦,如果把电压调高两倍,屏幕亮度并没有提高两倍啊!典型的CRT显示器的伽马曲线大致是一个伽马值为2.5的幂律曲线。显示器的这类伽马也称为displaygamma。由于这个问题的存在,那么图像捕捉设备就需要进行一个伽马校正,它们使用的伽马叫做encodinggamma。所以,一个完整的图像系统需要2个伽马值:-encodinggamma:它描述了encodingtransferfunction,即图像设备捕捉到的场景亮度值(sceneradiancevalues)和编码的像素值(encodedpixelvalues)之间的关系。-displaygamma:它描述了displaytransferfunction,即编码的像素值和显示的亮度(displayedradiance)之间的关系。如下图所示:而encodinggamma和displaygamma的乘积就是真个图像系统的end-to-endgamma。如果这个乘积是1,那么显示出来的亮度就是和捕捉到的真实场景的亮度是成比例的。上面的情景是对于捕捉的相片。那么对于我们渲染的图像来说,我们需要的是一个encodinggamma。如果我们没有用一个encodinggamma对shader的输出进行校正,而是直接显示在屏幕上,那么由于displaygamma的存在就会使画面失真。至此为止,就是龚大所说的伽马传说。由此,龚大认为全部的问题都出在CRT问题上,跟人眼没有任何关系。但是,在《Real-timeRendering》一书中,指出了这种乘积为1的end-to-endgamma的问题。看起来,乘积为1的话,可以让显示器精确重现原始场景的视觉条件。但是,由于原始场景的观察条件和显示的版本之间存在两个差异:1)首先是,我们能够显示的亮度值其实和真实场景的亮度值差了好几个数量级,说通俗点,就是显示器的精度根本达不到真实场景的颜色精度(大自然的颜色种类几乎是无穷多的,而如果使用8-bit的编码,我们只能显示256^3种颜色);2)这是一种称为surroundeffect的现象。在真实的场景中,原始的场景填充了填充了观察者的所有视野,而显示的亮度往往只局限在一个被周围环境包围的屏幕上。这两个差别使得感知对比度相较于原始场景明显下降了。也就是我们一开始说的,对光的灵敏度对不同亮度是不一样的。如下图所示(来源:Youtube:ColorisBroken):为了中和这种现象,所以我们需要乘积不是1的end-to-endgamma,来保证显示的亮度结果在感知上和原始场景是一致的。根据《Real-timeRendering》一书中,推荐的值在电影院这种漆黑的环境中为1.5,在明亮的室内这个值为1.125。个人电脑使用的一个标准叫sRGB,它使用的encodinggamma大约是0.45(也就是1/2.2)。这个值就是为了配合displaygamma为2.5的设备工作的。这样,end-to-endgamma就是0.45*2.5=1.125了。这意味着,虽然CRT的displaygamma是2.5,但我们使用的encodinggamma应该是1.125/2.5=1/2.2,而不是1/2.5。这样才能保证end-to-endgamma为1.125,从而在视觉上进行了补偿。虽然现在C...