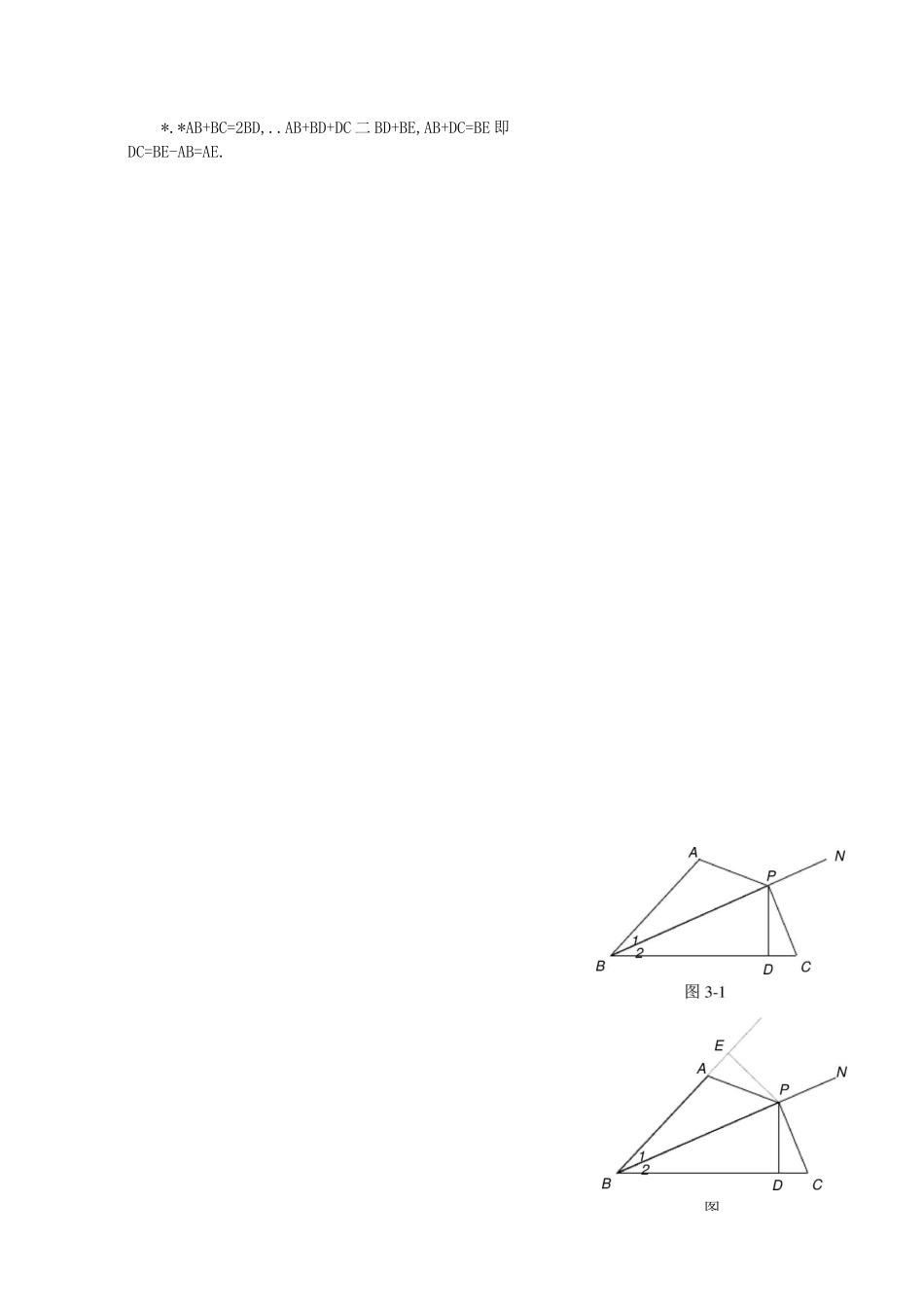
截长补短法例 1.已知,如图 1-1,在四边形 ABCD 中,BC>AB,AD=DC,BD 平分 ZABC.求证:ZBAD+ZBCD=180°.分析:因为平角等于 180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.证明:过点 D 作 DE 垂直 BA 的延长线于点 E,作 DF 丄 BC 于点 F,如图 1-2•••BD 平分 ZABC,・・・DE=DF,在 Rt△ADE 与 Rt△CDF 中,JDE 二 DFIAD 二 CD.•.RtAADE 今 RtACDF(HL),ZDAE=ZDCF.又 ZBAD+ZDAE=180°,.ZBAD+ZDCF=180O即 ZBAD+ZBCD=180°例 2.已知,如图 3-1,Z1=Z2,P 为 BN 上一点,且 PD 丄 BC 于点D,AB+BC=2BD.求证:ZBAP+ZBCP=180°.分析:与例 1 相类似,证两个角的和是 180°,可把它们移到一起,让它们是邻补角即证明 ZBCP=ZEAP,因而此题适用“补短”进行全等三角形的构造.证明:过点 P 作 PE 垂直 BA 的延长线于点 E,如图 3-2VZ1=Z2,且 PD 丄 BC,・・.PE=PD,在 Rt△BPE 与 Rt△BPD 中,PE 二 PDBP 二 BP.•・RtABPE^RtABPD(HL),・・・BE=BD.BADEC图图*.*AB+BC=2BD,..AB+BD+DC 二 BD+BE,AB+DC=BE 即DC=BE-AB=AE.图在 RtAAPE 与 RtACPD 中,'PE 二 PD