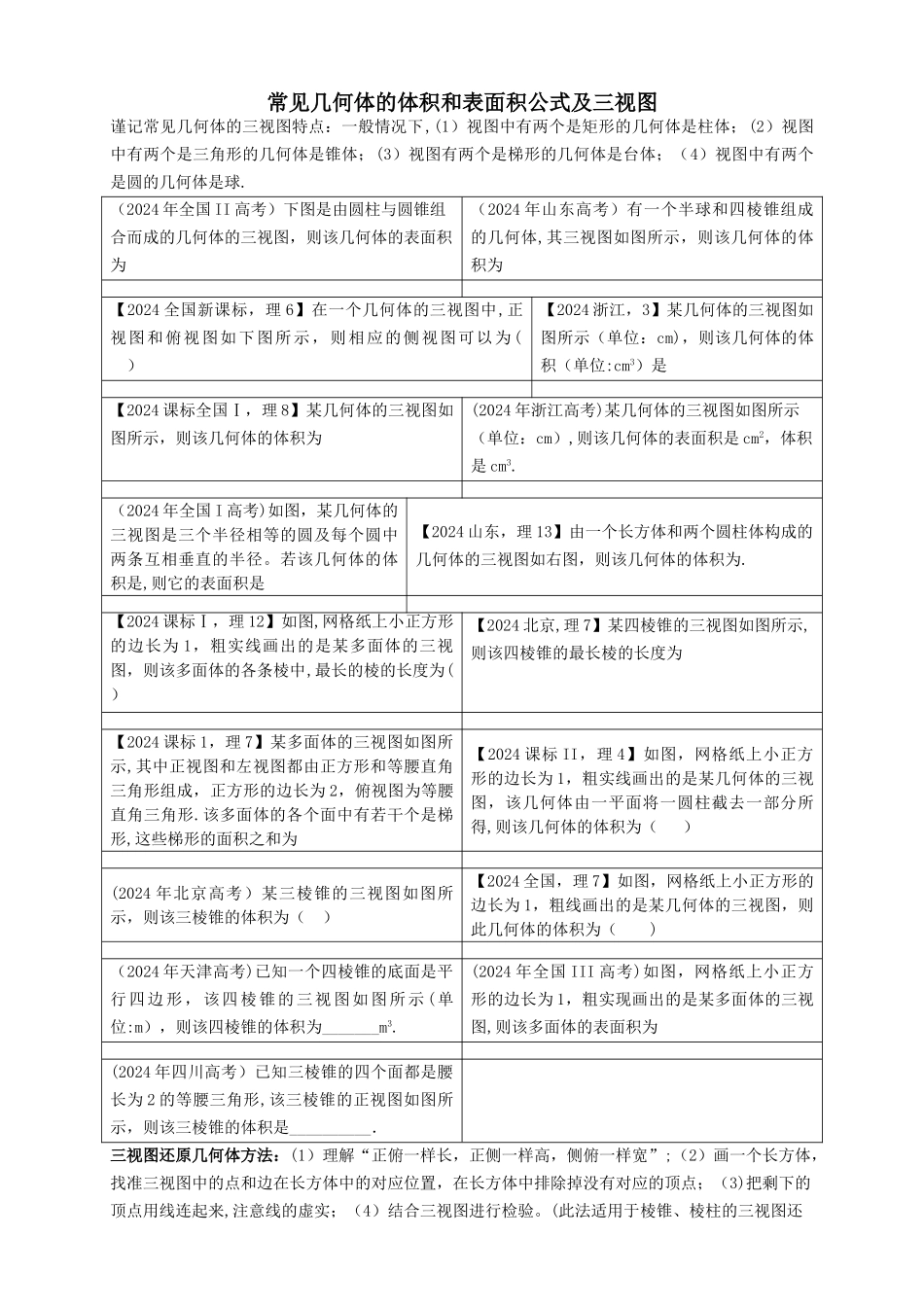
常见几何体的体积和表面积公式及三视图谨记常见几何体的三视图特点:一般情况下,(1)视图中有两个是矩形的几何体是柱体;(2)视图中有两个是三角形的几何体是锥体;(3)视图有两个是梯形的几何体是台体;(4)视图中有两个是圆的几何体是球. (2024 年全国 II 高考)下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(2024 年山东高考)有一个半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为【2024 全国新课标,理 6】在一个几何体的三视图中,正视图和俯视图如下图所示,则相应的侧视图可以为( )【2024 浙江,3】某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是【2024 课标全国Ⅰ,理 8】某几何体的三视图如图所示,则该几何体的体积为(2024 年浙江高考)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是 cm2,体积是 cm3.(2024 年全国 I 高考)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径。若该几何体的体积是,则它的表面积是【2024 山东,理 13】由一个长方体和两个圆柱体构成的几何体的三视图如右图,则该几何体的体积为.【2024 课标Ⅰ,理 12】如图,网格纸上小正方形的边长为 1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )【2024 北京,理 7】某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为【2024 课标 1,理 7】某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为 2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为【2024 课标 II,理 4】如图,网格纸上小正方形的边长为 1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )(2024 年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为( )【2024 全国,理 7】如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则此几何体的体积为( )(2024 年天津高考)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示 (单位:m),则该四棱锥的体积为_______m3.(2024 年全国 III 高考)如图,网格纸上小正方形的边长为 1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(2024 年四川高考)已知三棱锥的四个面都是腰长为 2 的等腰三角形,...