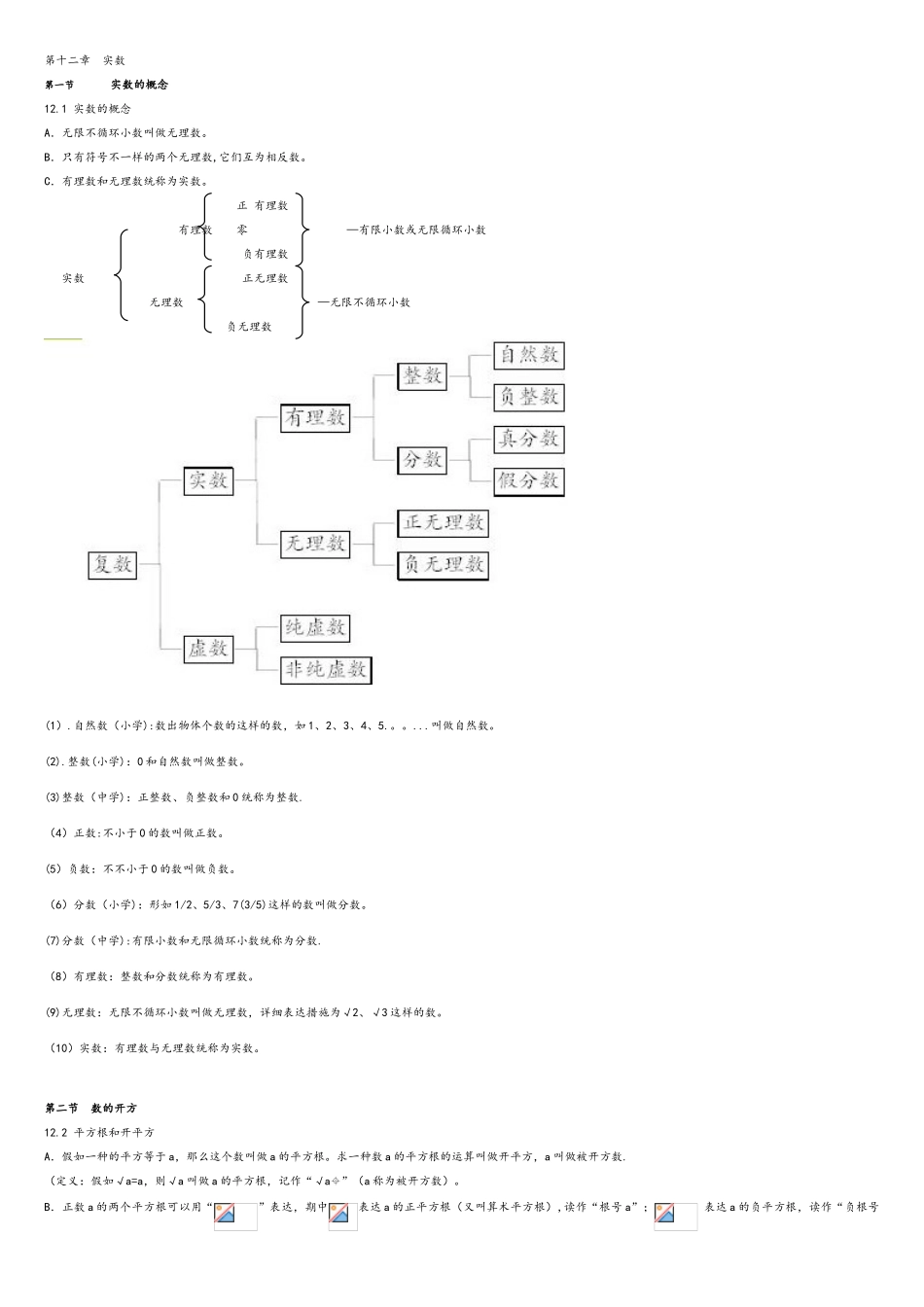
第十二章 实数第一节实数的概念12.1 实数的概念A.无限不循环小数叫做无理数。B.只有符号不一样的两个无理数,它们互为相反数。C.有理数和无理数统称为实数。 正 有理数 有理数 零 —有限小数或无限循环小数 负有理数 实数 正无理数 无理数 —无限不循环小数负无理数 (1).自然数(小学):数出物体个数的这样的数,如 1、2、3、4、5.。。...叫做自然数。(2).整数(小学):0 和自然数叫做整数。(3)整数(中学):正整数、负整数和 0 统称为整数.(4)正数:不小于 0 的数叫做正数。(5)负数:不不小于 0 的数叫做负数。(6)分数(小学):形如 1/2、5/3、7(3/5)这样的数叫做分数。(7)分数(中学):有限小数和无限循环小数统称为分数.(8)有理数:整数和分数统称为有理数。(9)无理数:无限不循环小数叫做无理数,详细表达措施为√2、√3 这样的数。(10)实数:有理数与无理数统称为实数。第二节 数的开方12.2 平方根和开平方A.假如一种的平方等于 a,那么这个数叫做 a 的平方根。求一种数 a 的平方根的运算叫做开平方,a 叫做被开方数.(定义:假如√a=a,则√a 叫做 a 的平方根,记作“√a”(a 称为被开方数)。B.正数 a 的两个平方根可以用“”表达,期中表达 a 的正平方根(又叫算术平方根),读作“根号 a”; 表达 a 的负平方根,读作“负根号a”.开平方和平方互为逆运算: 当 a>0 时 ()2= a (-)2= a (平方根等于自身的只有 0 ) 当 a≥0 时 = a = a 当 a<0 时 = -a零的平方根记作,=0注:一种正数的平方根的平方等于这个数。一种正(负)数的平方的正平方根等于这个数(这个数的相反数)。性质:正数的平方根有两个,它们互为相反数;0 的平方根是 0;负数没有平方根. 算术平方根:正数 a 的正的平方根叫做 a 的算术平方根,记作“√a”. 12。3 立方根和开立方A.假如一种数的立方等于 a,那么这个数叫做 a 的立方根,用“”表达,读作“三次根号 a”,a 叫做被开方数,“3”叫做根指数。求一种数 a 的立方根的运算叫做开立方.(定义:假如=a,则 x 叫做 a 的立方根,记作“”(a 称为被开方数)。 B.任意一种实数均有立方根,并且只有一种立方根。 =0 ( )3= a = a⑵、性质:正数有一种正的立方根;0 的立方根是 0;负数有一种负的立方根。 12.4 n 次方根A.假如一种数的 n 次方(n 是不小于 1 的整数)等于 a,那么这个数叫做 a ...