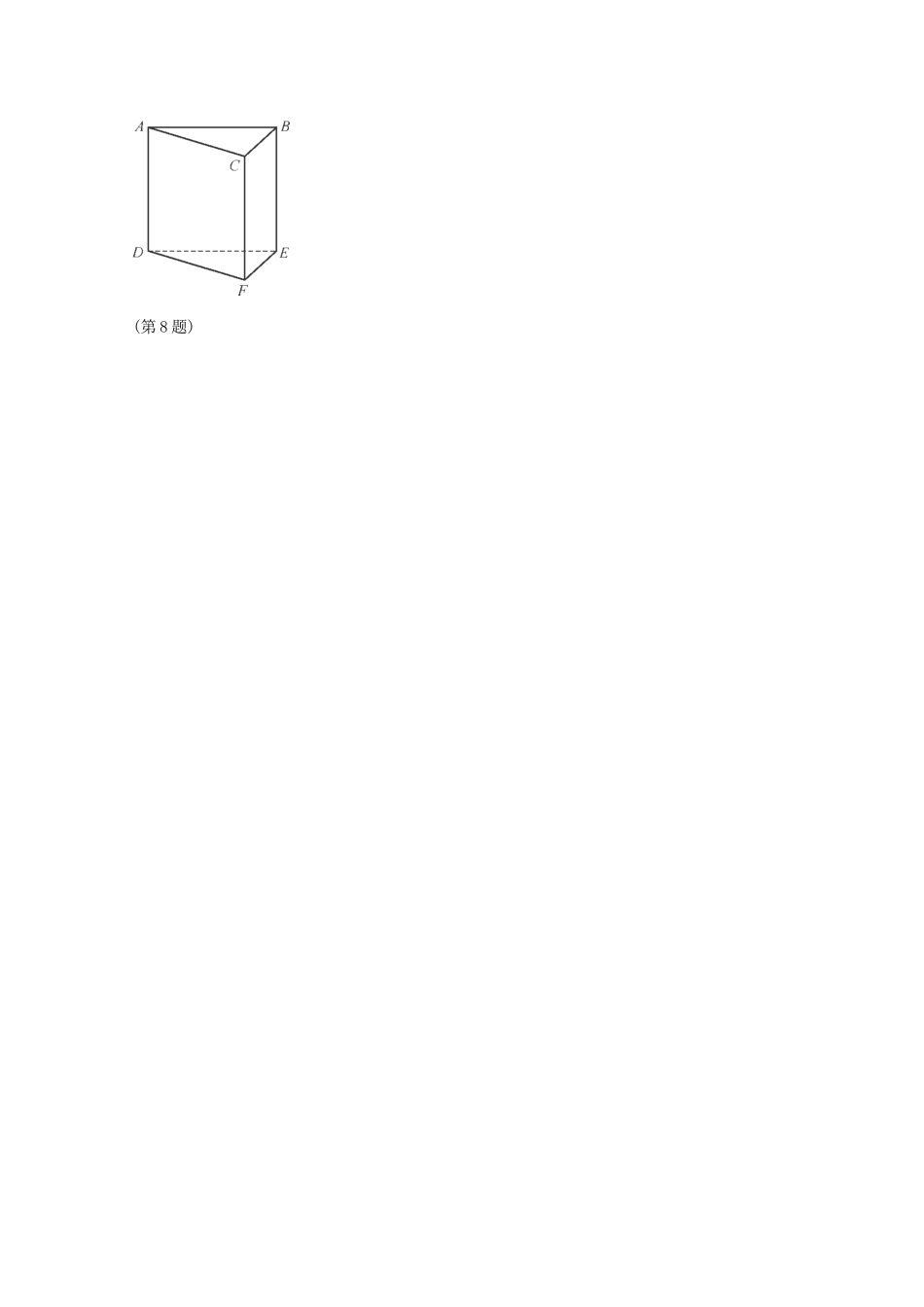
数学高考疯狂时刻引领状元之路:数学归纳法1. 求证:n3+5n(n∈N*)能被 6 整除.2.设 n∈N*且 n≥2,证明:(a1+a2+…+an)2=++…++2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].3. 在数列{an}中,a1=,an+1=(n∈N*),用数学归纳法证明:an>2(n∈N*).4. 试比较 2n+2 与 n2 的大小(n∈N*),并用数学归纳法证明你的结论.5. 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0.(第 8 题)第 3 讲 数学归纳法1. (1) 当 n=1 时,n3+5n=6 能被 6 整除.(2) 假设当 n=k(k≥1,且 k∈N*)时,k3+5k 能被 6 整除;则当 n=k+1 时,(k+1)3+5(k+1)=k3+3k2+3k+1+5k+5=k3+5k+3k(k+1)+6.由假设知 k3+5k 能被 6 整除,而 3k(k+1),6 也能被 6 整除,因此(k+1)3+5(k+1)能被 6 整除.由(1)(2)可知, 命题对任意 n∈N*都成立.2. (1) 当 n=2 时,有(a1+a2)2=++2a1a2,命题成立.(2) 假设当 n=k(k≥2)时,命题成立,即(a1+a2+…+ak)2=++…++2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]成立;那么,当 n=k+1 时,有(a1+a2+…+ak+ak+1)2=(a1+a2+…+ak)2+2(a1+a2+…+ak)ak+1+=++…++2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]+2(a1+a2+…+ak)ak+1+=++…+++2[a1(a2+a3+…+ak+ak+1)+a2(a3+a4+…+ak+ak+1)+…+akak+1],因此当 n=k+1 时,命题也成立.根据(1)和(2),可知命题对任意的 n∈N*且 n≥2 都成立.3. (1) 当 n=1 时,a1=>2,不等式成立.(2) 假设当 n=k 时等式成立,即 ak>2(k∈N*),则 ak+1-2=-2=>0,因此 ak+1>2,因此当 n=k+1 时,不等式也成立.综合(1)(2),不等式对所有正整数都成立.4. 当 n=1 时,21+2=4>n2=1;当 n=2 时,22+2=6>n2=4;当 n=3 时,23...