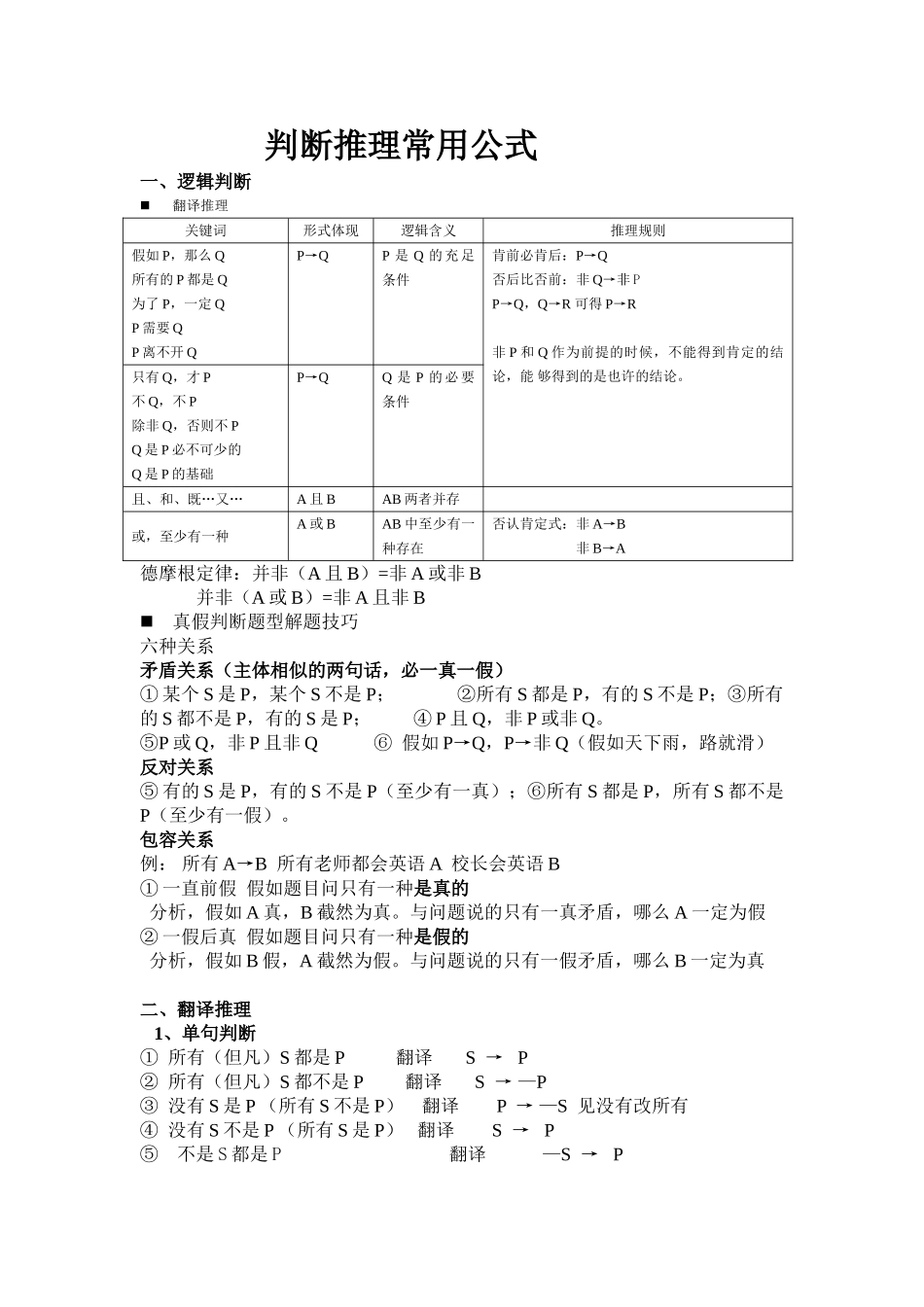
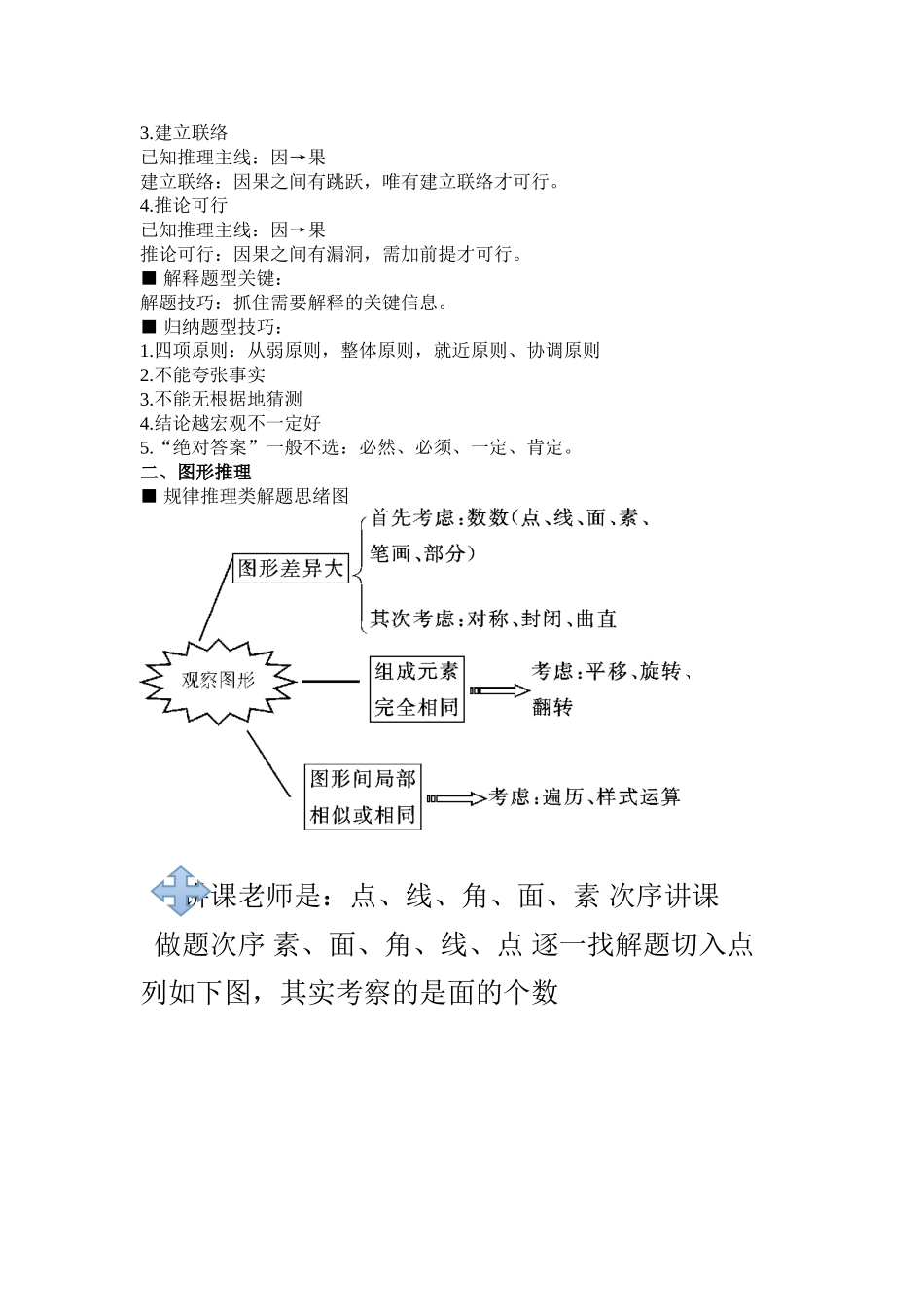
判断推理常用公式一、逻辑判断翻译推理关键词形式体现逻辑含义推理规则假如 P,那么 Q所有的 P 都是 Q为了 P,一定 QP 需要 QP 离不开 QP→QP 是 Q 的 充 足条件肯前必肯后:P→Q否后比否前:非 Q→非 PP→Q,Q→R 可得 P→R非 P 和 Q 作为前提的时候,不能得到肯定的结论,能 够得到的是也许的结论。只有 Q,才 P不 Q,不 P除非 Q,否则不 PQ 是 P 必不可少的Q 是 P 的基础P→QQ 是 P 的 必 要条件且、和、既…又…A 且 BAB 两者并存或,至少有一种A 或 BAB 中至少有一种存在否认肯定式:非 A→B非 B→A德摩根定律:并非(A 且 B)=非 A 或非 B 并非(A 或 B)=非 A 且非 B真假判断题型解题技巧六种关系矛盾关系(主体相似的两句话,必一真一假)① 某个 S 是 P,某个 S 不是 P; ②所有 S 都是 P,有的 S 不是 P;③所有的 S 都不是 P,有的 S 是 P; ④ P 且 Q,非 P 或非 Q。⑤P 或 Q,非 P 且非 Q ⑥ 假如 P→Q,P→非 Q(假如天下雨,路就滑)反对关系⑤ 有的 S 是 P,有的 S 不是 P(至少有一真);⑥所有 S 都是 P,所有 S 都不是P(至少有一假)。包容关系例: 所有 A→B 所有老师都会英语 A 校长会英语 B① 一直前假 假如题目问只有一种是真的 分析,假如 A 真,B 截然为真。与问题说的只有一真矛盾,哪么 A 一定为假② 一假后真 假如题目问只有一种是假的 分析,假如 B 假,A 截然为假。与问题说的只有一假矛盾,哪么 B 一定为真二、翻译推理 1、单句判断① 所有(但凡)S 都是 P 翻译 S → P② 所有(但凡)S 都不是 P 翻译 S → —P ③ 没有 S 是 P (所有 S 不是 P) 翻译 P → —S 见没有改所有④ 没有 S 不是 P (所有 S 是 P) 翻译 S → P⑤ 不是 S 都是 P 翻译 —S → P ⑥ 不是 S 都不是 P 翻译 —S → —P 2、否认关系1、并非所有 A 都是 B 等价于 有的 A 不是 B (并非所有换成有的,是换不是) 2、并非有的 A 是 B 等价于 所有 A 都不是 B (并非有的换成所有,是换成不是) 3、等价关系1、所有的 A 都不是 B 等价于 所有的 B 都不是 A2、有的 A 是 B 等价于 有的 B 是啊五个解题环节① 符号化;②找关系(六种关系);③推知其他项真假;④根据其他项真假,得出真实状况;⑤...