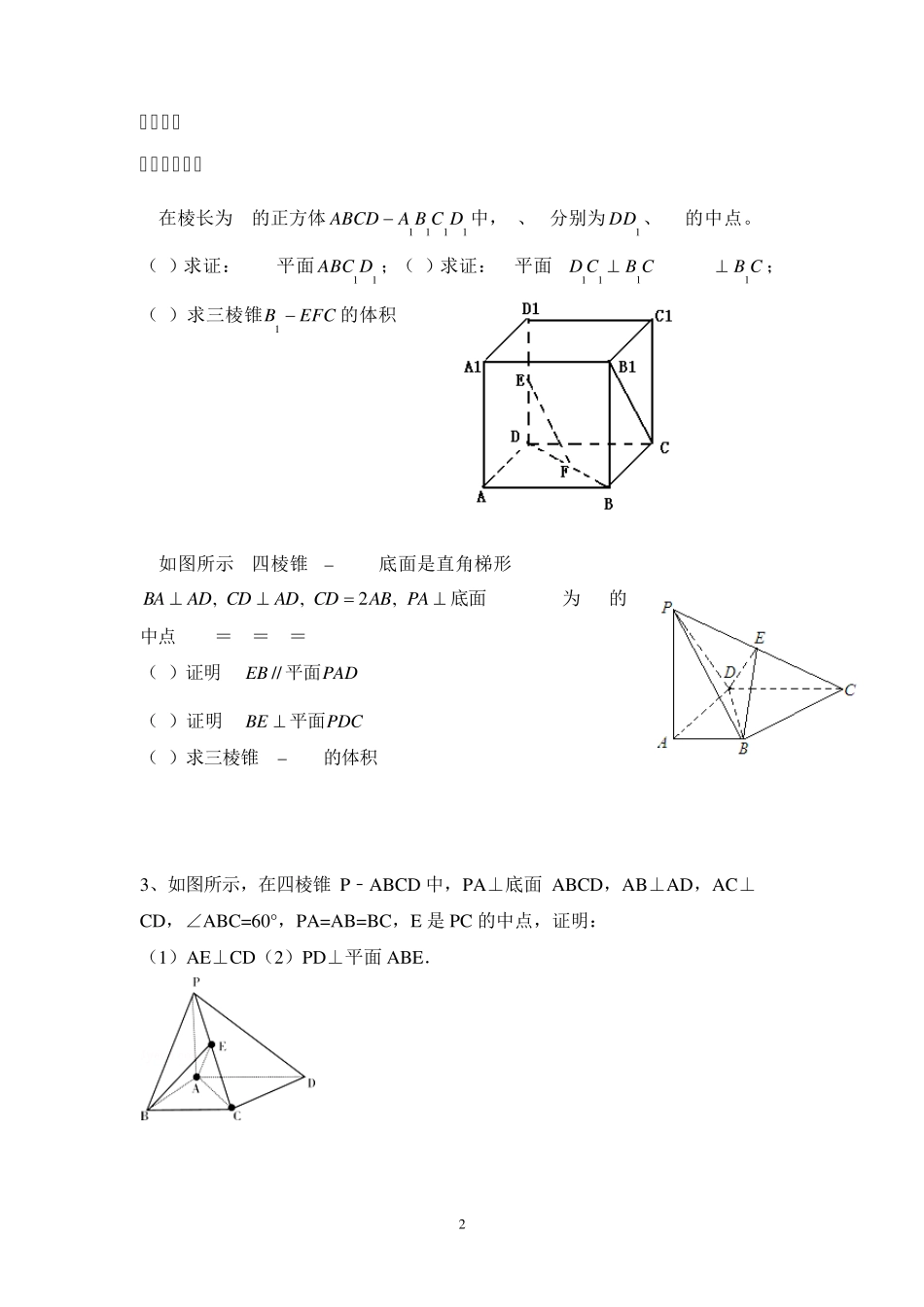
1 立体几何证明 【知识梳理】 1 . 直线与平面平行 判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行线面平行”) 性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行线线平行”) 2 ..直线与平面垂直 判定定理一 如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直线面垂直”) 判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面. 性质 1 .如果一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线。 (线面垂直线线垂直) 性质 2 :如果两条直线同垂直于一个平面,那么这两条直线平行. 三。平面与平面 空间两个平面的位置关系:相交、平行. 1 . 平面与平面平行 判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(“线面平行面面平行”) 2 . 两个平面垂直 判定定理:如果一条直线与一个平面垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直面面垂直”) 性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.(面面垂直线面垂直) 2 知识点一 【例题精讲】 1.在棱长为2的正方体1111DCBAABCD 中,E、F分别为1DD 、DB的中点。 (1)求证:EF//平面11DABC;(2)求证: 平面B11D CCB1 EFCB1; (3)求三棱锥EFCB 1的体积V. 2.如图所示, 四棱锥P ABCD底面是直角梯形, ,,2,BAAD CDAD CDABPA 底面ABCD, E为PC的中点, PA=AD=AB=1. (1)证明: //EBPAD平面; (2)证明: BEPDC 平面; (3)求三棱锥B PDC的体积V. 3、如图所示,在四棱锥P﹣ABCD 中,PA⊥底面 ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E 是PC 的中点,证明: (1)AE⊥CD(2)PD⊥平面ABE. 3 4、.如图,三棱柱ABC﹣A1B1C1 中,CA=CB,AB=AA1,∠BAA1=60°(Ⅰ)证明:AB⊥A1C; 练习 1、如图,菱形ABCD 与等边△PAD 所在的平面相互垂直,AD=2,∠DAB=60°. (Ⅰ)证明:AD⊥PB;(Ⅱ)求三棱锥C﹣PAB 的高. 2.如图1-4 所示,△ABC 和△BCD 所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G 分别为 AC,DC,AD 的中点.求证:EF⊥平面BCG; 3.如图1-1 所示,三...