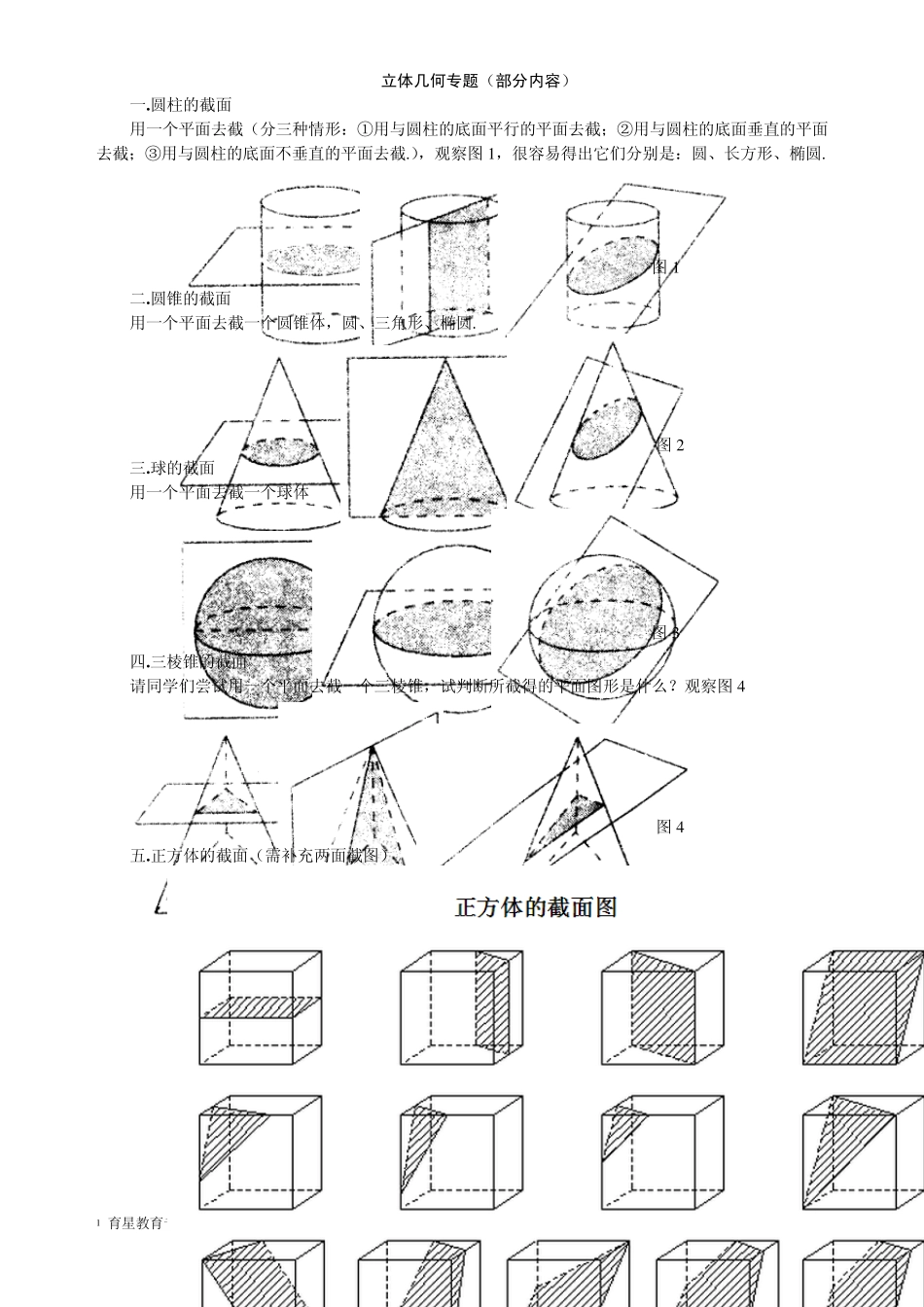
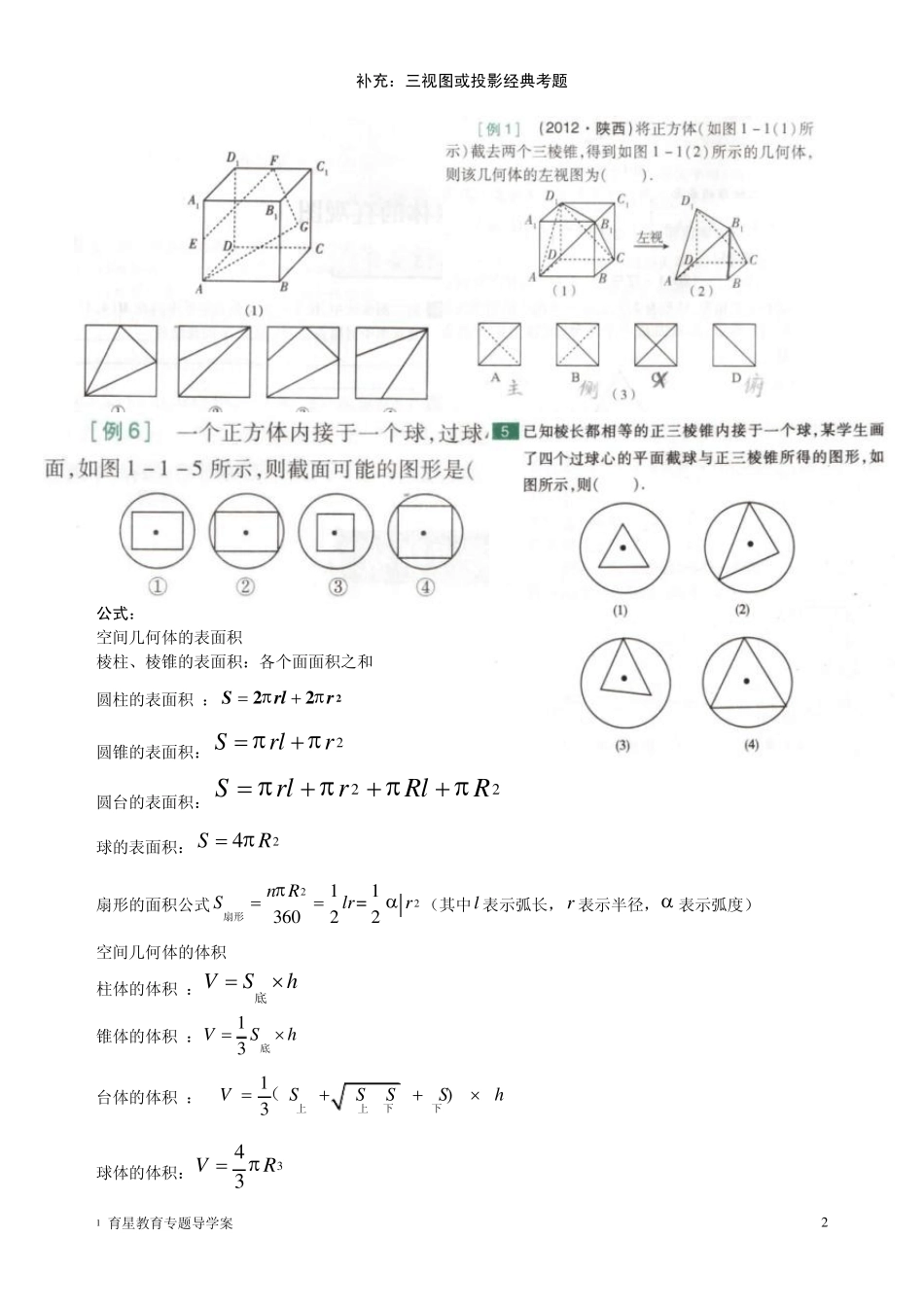
1 育星教育专题导学案 1 立体几何专题(部分内容) 一.圆柱的截面 用一个平面去截(分三种情形:①用与圆柱的底面平行的平面去截;②用与圆柱的底面垂直的平面去截;③用与圆柱的底面不垂直的平面去截.),观察图 1 ,很容易得出它们分别是:圆、长方形、椭圆. 图 1 二.圆锥的截面 用一个平面去截一个圆锥体,圆、三角形、椭圆. 图 2 三.球的截面 用一个平面去截一个球体 图 3 四.三棱锥的截面 请同学们尝试用一个平面去截一个三棱锥,试判断所截得的平面图形是什么?观察图 4 图 4 五.正方体的截面(需补充两面截图) 1 育星教育专题导学案 2 补充:三视图或投影经典考题 公式: 空间几何体的表面积 棱柱、棱锥的表面积:各个面面积之和 圆柱的表面积 :222Srlr 圆锥的表面积:2Srlr 圆台的表面积:22SrlrRlR 球的表面积:24SR 扇形的面积公式2211=36022n RSlrr扇形(其中l 表示弧长,r表示半径, 表示弧度) 空间几何体的体积 柱体的体积 :VSh底 锥体的体积 :13VSh底 台体的体积 : 1)3VSSSSh下下上上( 球体的体积:343VR 1 育星教育专题导学案 3 空间几何体的三视图和直观图:正俯长相等、正侧高相同、俯侧宽一样 正视图:光线从几何体的前面向后面正投影,得到的投影图。 侧视图:光线从几何体的左边向右边正投影,得到的投影图。 俯视图:光线从几何体的上面向右边正投影,得到的投影图。 1 、线线平行的判断: (1 )、平行于同一直线的两直线平行。 (3 )、如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。 (6 )、如果两个平行平面同时和第三个平面相交,那么它们的交线平行。 (1 2 )、垂直于同一平面的两直线平行。 2 、线线垂直的判断: (7 )、在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。 (8 )、在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直。 (1 0 )、若一直线垂直于一平面,这条直线垂直于平面内所有直线。 补充:一条直线和两条平行直线中的一条垂直,也必垂直平行线中的另一条。 3 、线面平行的判断: (2 )、如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。 (5 )、两个平面平行,其中一个平面内的直线必平...