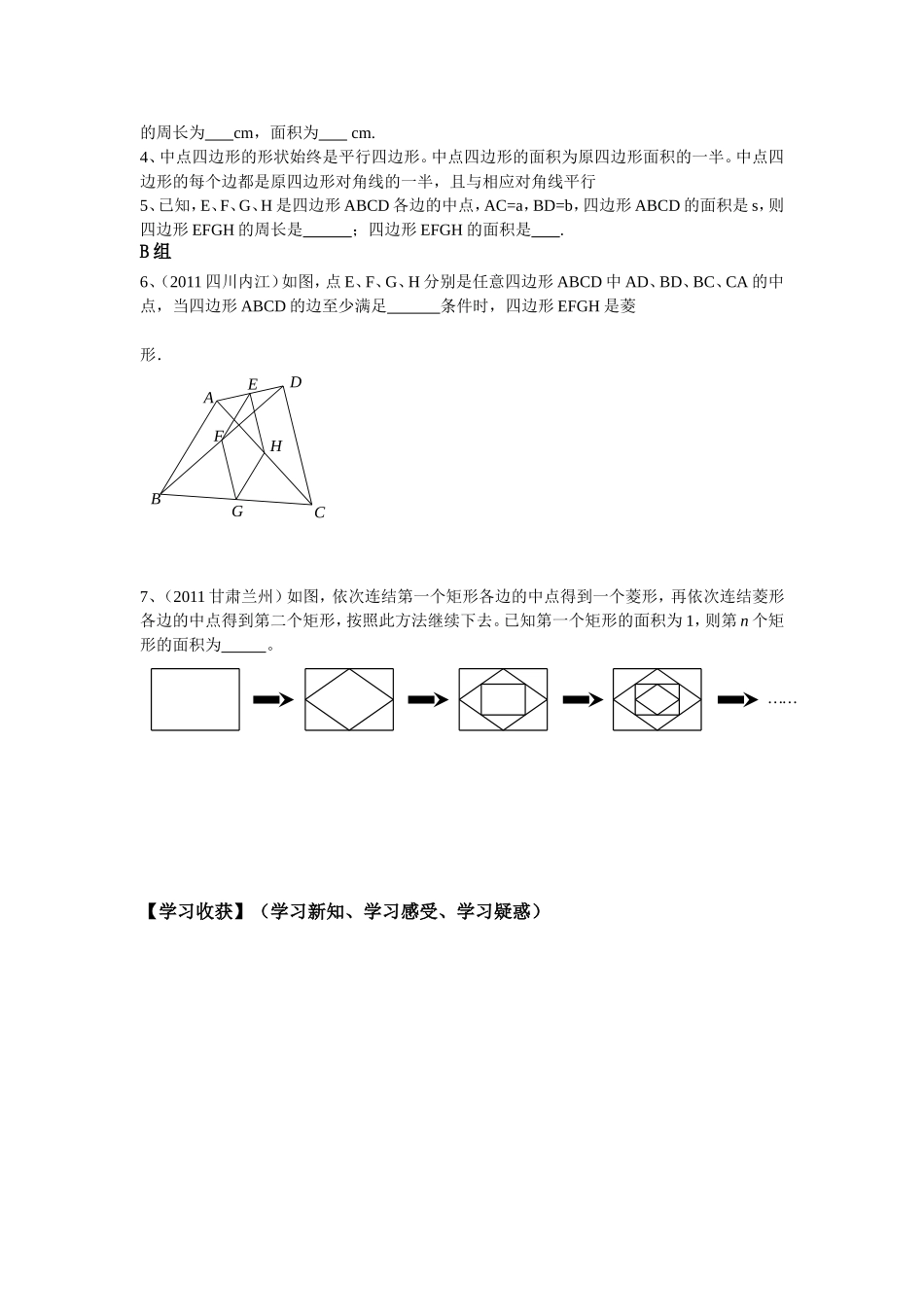
北师版九年级数学上册学案9第三章证明(三)2.特殊的平行四边形—中点四边形【学习目标】1、经历探索、猜想、证明的过程,进一步发展推理论证的能力,2、掌握中点四边形的形状,熟悉特殊平行四边形的判定技能以及灵活运用三角形中位线定理的技能;3、通过综合法的证明过程,体会证明的有关思维方法;【学习重点】目标2【学习难点】目标3【学习过程】一、旧知回顾1、三角形的中位线具有哪些性质?2、平行四边形、矩形、菱形、正方形在对角线方面具有哪些性质?3、矩形、菱形、正方形的判定方法有哪些?4、前面已探讨过,依次连接任意四边形各边的中点可以得到一个什么四边形?画图,写出推导过程。从证明过程中可知:中点四边形的边与原四边形的有密切关系。二、预习导学拓展:任意连接等腰梯形各边中点得到一个什么图形,它们相同吗?回味刚才的证明过程,想一想:要使中点四边形是菱形,原四边形一定要是矩形吗?由此可得:只要原四边形的两条对角线,就能使中点四边形是菱形。3.依次连结菱形四边的中点能得到一个图形。先猜一猜,再推导.1.依次连接平行四边形四边的中点得到一个什么图形?先猜一猜,再推导。已知在菱形ABCD中,点A1、B1、C1、D1分别是菱形四条边的中点,拓展:连接个对角线互相垂直的四边形的各边中点,得到一个什么图形,它们相同吗?回味刚才的证明过程,想一想:要使中点四边形是矩形,原四边形一定要是菱形吗?由此可得:只要原四边形的两条对角线,就能使中点四边形是矩形。4.依次连接正方形各边的中点.能得到—个图形。先猜一猜,再推导.已知在正方形ABCD中,点A1、B1、C1、D1分别是正方形四条边的中点。拓展:连接一个对角线互相垂直且相等的四边形的各边中点,得到一个什么图形,它们相同吗?讨论一下:要使中点四边形是正方形,原四边形要符合的条件是。5.思考并讨论:通过实践、讨论加猜想验证,我们发现,四个动手操作中的新四边形的形状不完全相同,从上面的研究过程中,你发现了什么规律?请总结一下新四边形的形状与哪些线段有关?有什么样的关系?得出:所得的四边形的形状与原四边形的关系和关系有关.6.大家来想一想:连结哪些四边形各边中点所得到的图形是矩形呢?菱形呢?若四边形的对角线相等,则连结这个四边形各边中点所得到的图形就是.若四边形的对角线互相垂直,那么连接这个四边形各边的中点所得到的图形就是.若四边形的对角线互相垂直且相等,那么连接这个四边形各边的中点所得到的图形就是.【达标检测】A组1、顺次连接四边形各边中点,所得的图形是;顺次连接对角线的四边形的各边中点所得的图形是矩形;顺次连接对角线的四边形的各边中点所得的四边形是菱形;顺次连接对角线的四边形的各边中点所得的四边形是正方形.2、顺次连接一个四边形的各边中点,得到一个矩形,则下列四边形满足条件的是()①平行四边形②菱形③等腰梯形④对角线互相垂直的四边形A.①③B.②③C.③④D.②④3、正方形ABCD的周长为16cm,顺次连接正方形ABCD各边中点,得到四边形EFGH,则它的周长为cm,面积为cm.4、中点四边形的形状始终是平行四边形。中点四边形的面积为原四边形面积的一半。中点四边形的每个边都是原四边形对角线的一半,且与相应对角线平行5、已知,E、F、G、H是四边形ABCD各边的中点,AC=a,BD=b,四边形ABCD的面积是s,则四边形EFGH的周长是;四边形EFGH的面积是.B组6、(2011四川内江)如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足条件时,四边形EFGH是菱形.7、(2011甘肃兰州)如图,依次连结第一个矩形各边的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去。已知第一个矩形的面积为1,则第n个矩形的面积为。【学习收获】(学习新知、学习感受、学习疑惑)ABCDEFGH……