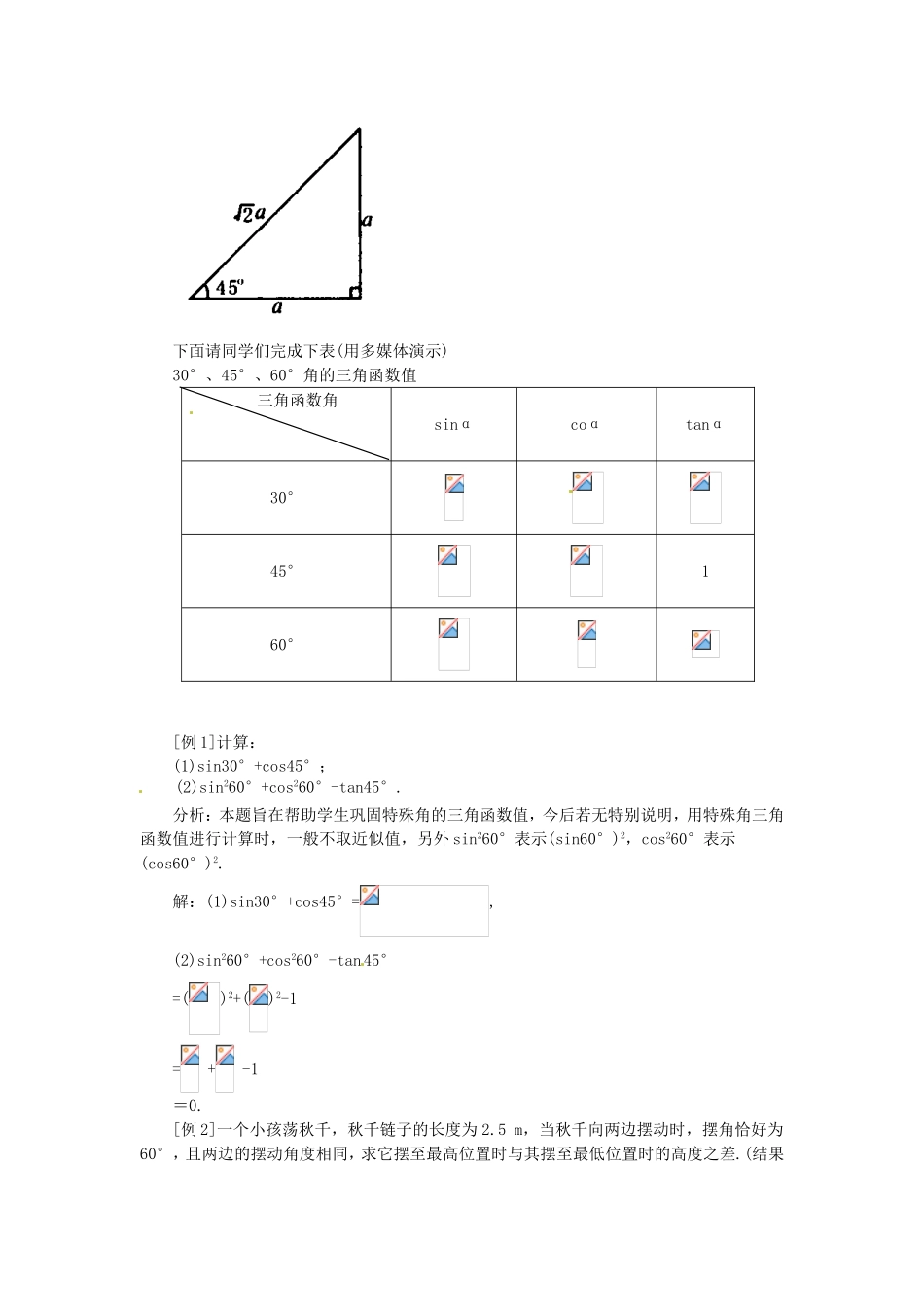
1.1锐角三角函数1.探索直角三角形中锐角三角函数值与三边之间的关系,掌握三角函数的定义。2.能够进行30°、45°、60°角的三角函数值的计算.3.经历探索三角函数的过程,发展学生观察、分析、发现的能力.教学重点三角函数的定义教学难点特殊三角函数值.一、新课导入如图是两个自动扶梯,甲、乙两人分别从1、2号自动扶梯上楼,谁先到达楼顶?如果AB和A′B′相等而∠α和∠β大小不同,那么它们的高度AC和A′C′相等吗?AB、AC、BC与∠α,A′B′、A′C′、B′C′与∠β之间有什么关系呢?二、探索新知1.三角函数的定义在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边的比也随之确定.∠A的对边与邻边的比叫做∠A的正弦(sine),记作sinA,即sinA=∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即cosA=∠A的对边与∠A的邻边的比叫做∠A的正切(tangent),记作tanA,即锐角A的正弦、余弦和正切统称∠A的三角函数.注意:sinA,cosA,tanA都是一个完整的符号,单独的“sin”没有意义,其中A前面的“∠”一般省略不写。例1如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,求∠A,∠B的正弦,余弦和正切.分析:由勾股定理求出AC的长度,再根据直角三角形中锐角三角函数值与三边之间的关系求出各函数值。师:观察以上计算结果,你发现了什么?明确:sinA=cosB,cosA=sinB,tanA·tanB=12.探索30°、45°、60°角的三角函数值.观察一副三角尺,其中有几个锐角?它们分别等于多少度?一副三角尺中有四个锐角,它们分别是30°、60°、45°、45°.sin30°等于多少呢?sin30°=.sin30°表示在直角三角形中,30°角的对边与斜边的比值,与直角三角形的大小无关.我们不妨设30°角所对的边为a(如图所示),根据“直角三角形中30°角所对的边等于斜边的一半”的性质,则斜边等于2a.根据勾股定理,可知30°角的邻边为a,所以sin30°=.cos30°=.tan30°=求60°的三角函数值可以利用求30°角三角函数值的三角形.因为30°角的对边和邻边分别是60°角的邻边和对边.利用上图,很容易求得sin60°=,cos60°=,tan60°=.也可以利用上节课我们得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知sin60°=cos(90°-60°)=cos30°=cos60°=sin(90°-60°)=sin30°=.含45°角的直角三角形是等腰直角三角形.(如图)设其中一条直角边为a,则另一条直角边也为a,斜边a.由此可求得sin45°=,cos45°=,tan45°=下面请同学们完成下表(用多媒体演示)30°、45°、60°角的三角函数值三角函数角sinαcoαtanα30°45°160°[例1]计算:(1)sin30°+cos45°;(2)sin260°+cos260°-tan45°.分析:本题旨在帮助学生巩固特殊角的三角函数值,今后若无特别说明,用特殊角三角函数值进行计算时,一般不取近似值,另外sin260°表示(sin60°)2,cos260°表示(cos60°)2.解:(1)sin30°+cos45°=,(2)sin260°+cos260°-tan45°=()2+()2-1=+-1=0.[例2]一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.(结果精确到0.01m)分析:引导学生自己根据题意画出示意图,培养学生把实际问题转化为数学问题的能力.解:根据题意(如图)可知,∠BOD=60°,OB=OA=OD=2.5m,∠AOD=×60°=30°,∴OC=OD·cos30°=2.5×≈2.165(m).∴AC=2.5-2.165≈0.34(m).所以,最高位置与最低位置的高度约为0.34m.做一做1.计算:(1)sin60°-tan45°;(2)cos60°+tan60°;(3)sin45°+sin60°-2cos45°.解:(1)原式=-1=;(2)原式=+=(3)原式=×+×;=2.某商场有一自动扶梯,其倾斜角为30°.高为7m,扶梯的长度是多少?解:扶梯的长度为=14(m),所以扶梯的长度为14m.三、归纳小结1.在RtΔABC中,设∠C=900,∠α为RtΔABC的一个锐角,则∠α的正弦,∠α的余弦,∠α的正切2.一般地,在Rt△ABC中,当∠C=90°时,sinA=cosB,cosA=sinB,tanA·tanB=13.特殊角的三角函数值:sin30°=,sin45°=,sin60°=;cos30°=,cos45°=,cos60°=;tan30°=,tan45°=1,tan60°=.请完成本作业本对应练习!