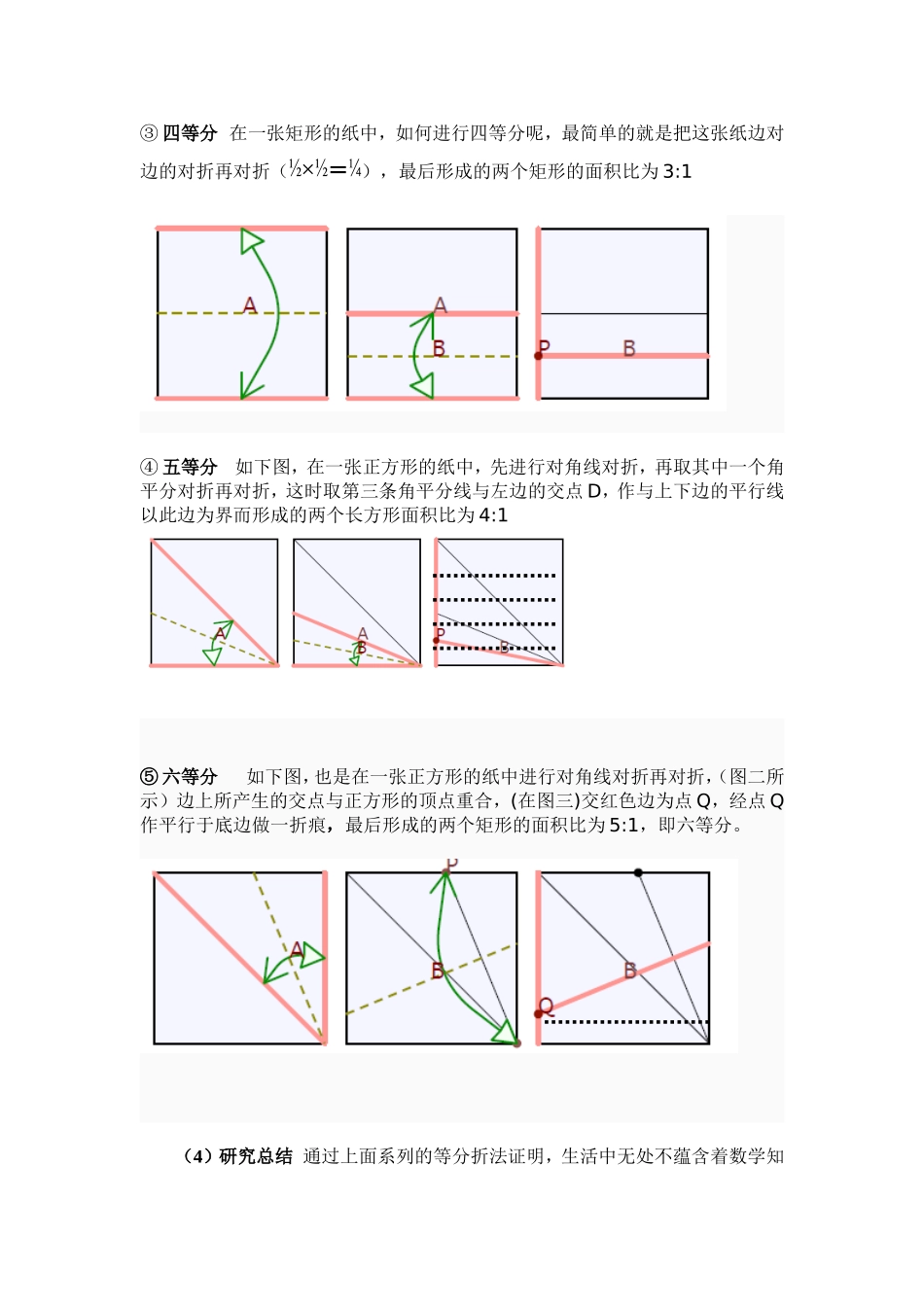
《折纸中的数学》(1)课题的背景折纸起源于中国,而我酷爱折纸,因为折纸又称之为“工艺折纸”,是一种以纸张折成各种不同形状的艺术活动。如今折纸的发展不只是儿童的玩具,也是一种有益身心、开发智力和思维的活动。凭着我对折纸的热爱,在无数次的折纸实践中,我发现其实折纸与数学存在着密不可分的关系,在折纸中用到许多数学知识。(2)此小课题的目的如何将一张平面的纸张通过折叠成有空间概念的模型,比如幸运星、千纸鹤、或是纸飞机等等?这就是需要运用到折纸中最基础的“将一条线N等分”的方法,可是如何将一条直线进行多次等分,比如2、3、4、5、6等分呢?(3)研究的内容和步骤ABDCOEFG③四等分在一张矩形的纸中,如何进行四等分呢,最简单的就是把这张纸边对边的对折再对折(½×½=¼),最后形成的两个矩形的面积比为3:1④五等分如下图,在一张正方形的纸中,先进行对角线对折,再取其中一个角平分对折再对折,这时取第三条角平分线与左边的交点D,作与上下边的平行线以此边为界而形成的两个长方形面积比为4:1⑤六等分如下图,也是在一张正方形的纸中进行对角线对折再对折,(图二所示)边上所产生的交点与正方形的顶点重合,(在图三)交红色边为点Q,经点Q作平行于底边做一折痕,最后形成的两个矩形的面积比为5:1,即六等分。(4)研究总结通过上面系列的等分折法证明,生活中无处不蕴含着数学知识。数学寓于折纸之中,对数学的了解总然会在折纸中增加人的能力和创造力。当折叠纸张的时候,很自然地会出现许多几何的概念和代数概念。诸如:正方形、矩形、直角三角形、全等、对角线、中点、内接、面积、梯形、垂直平分线。在每一次折纸时,用数学的眼光去观察,会发现折纸中包含着许许多多的数学奥秘。折纸凭借着折叠时产生的几何形的连续变化而形成物象。任何一张纸都是个几何图形折叠后产生新的几何图形,组合后可称为几何体。这中间蕴含着数学、几何、测绘造型等多学科、综合知识的运用。通过各种几何图形的折叠实践,可以领悟出角等分和边等分是使用最为普遍的方法。也发现了折叠中常见的几种类型:线线重合折叠、点线重合折叠、点点重合折叠、沿对称轴折叠。只有掌握了上面例举的几种方法,才能折出各种各样的纸模型来。而且事实证明,如果没有很好的掌握数学知识,稍有偏差就成不了等分,所折的出来的作品就会不规则,影响效果和美感。所以想做好折纸这项手工艺术活,也必须认真学好数学,研究数学的规律,才会创造出更多的新作品来。通过折纸可启发我们的创造力和逻辑思维,更可促进手脑的协调。折纸还可以丰富我们的生活,使我们的生活变得更加绚烂多彩。