各类刚体转动惯量公式的推导

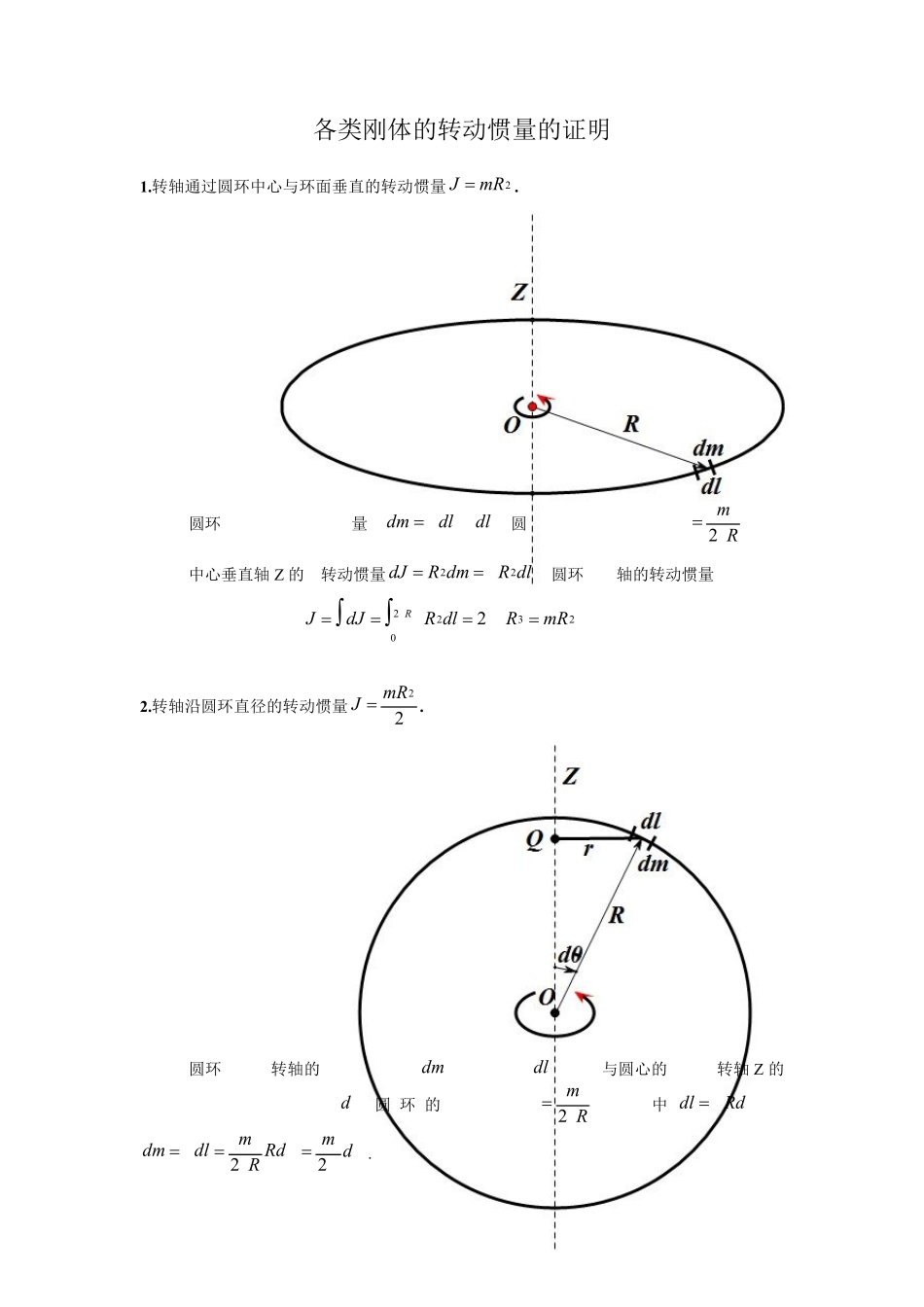
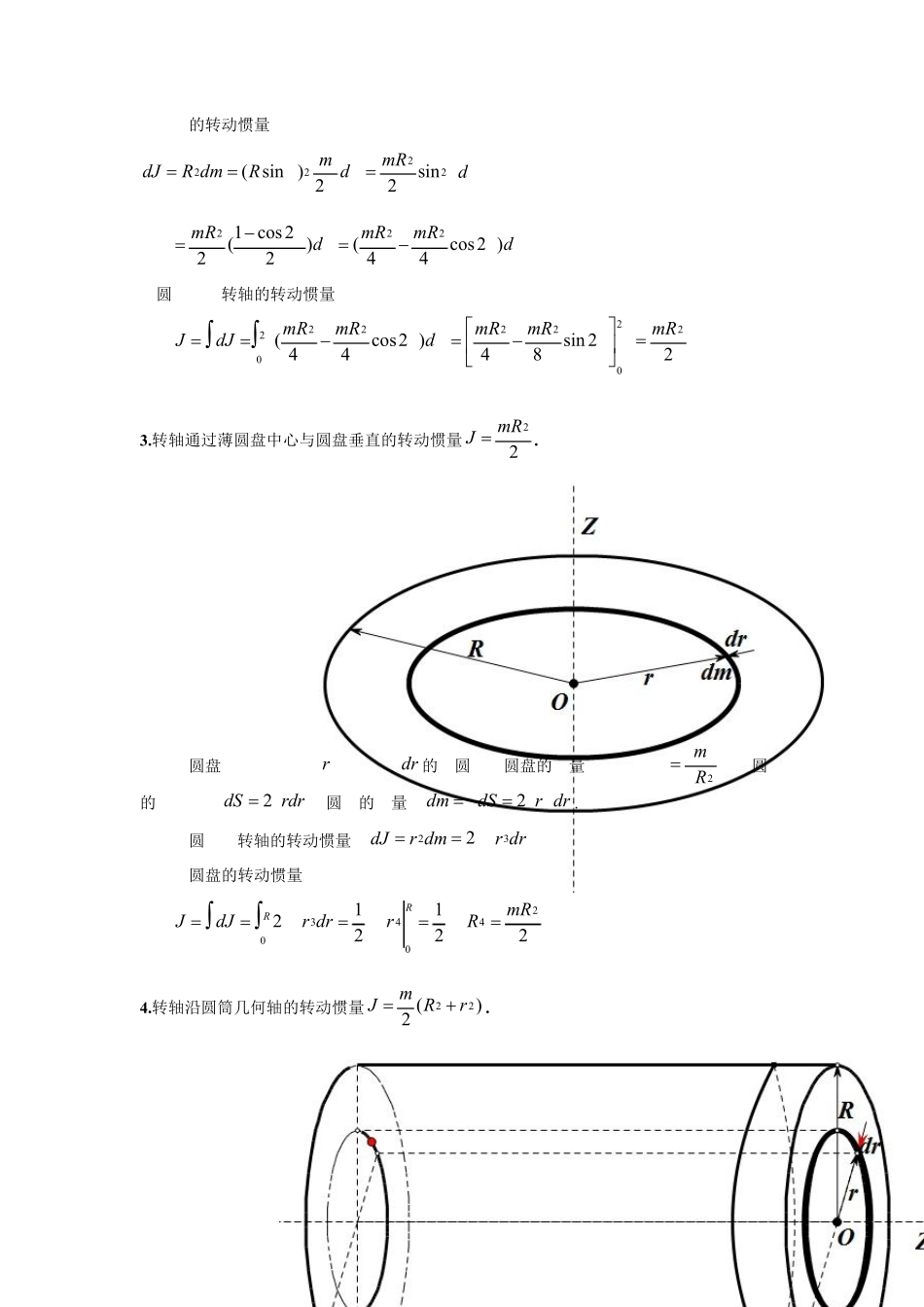
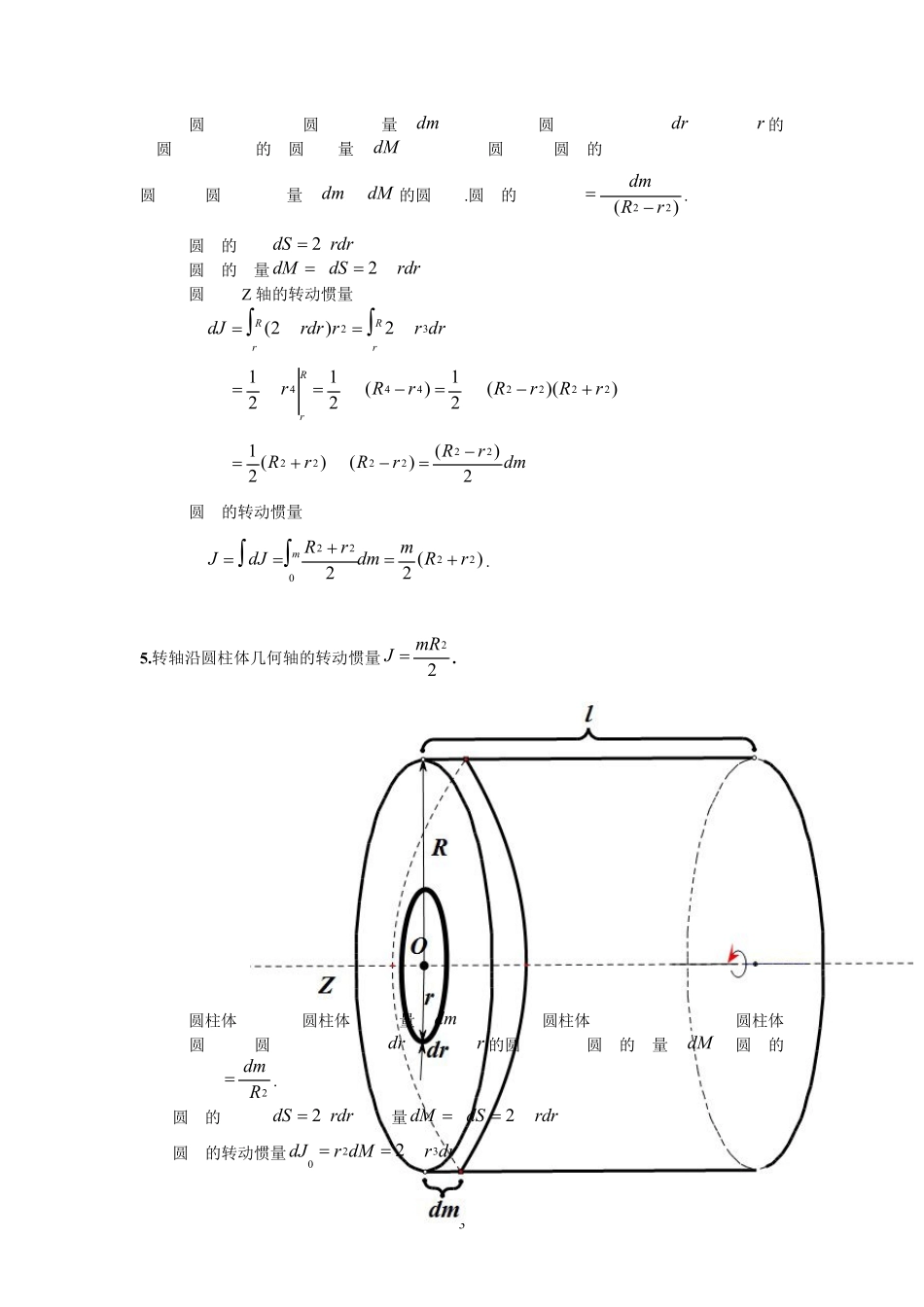
1各类刚体的转动惯量的证明1.转轴通过圆环中心与环面垂直的转动惯量2m RJ .在圆环上取一质元，其质量为dldm，dl 为圆弧元，为线密度（Rm 2）。该质元对中心垂直轴Z 的元转动惯量dlRdmRdJ22，圆环对该轴的转动惯量为220322m RRdlRdJJR 2.转轴沿圆环直径的转动惯量22m RJ .在圆环上靠近转轴的一处取一质元 dm ，其弧长为 dl ，质元与圆心的连线和转轴Z 的夹 角 （ 微 夹 角 ） 为d圆环的线 密 度Rm 2， 其 中dlRd，dmRdRmdldm22.2该质元的转动惯量为dmRdmRdmRdJ2222sin22)sin(dmRmRdmR)2cos44()22cos1(2222则圆环对该转轴的转动惯量为22sin84)2cos44(220202222mRmRmRdmRmRdJJ3.转轴通过薄圆盘中心与圆盘垂直的转动惯量22mRJ .在圆盘上取一半径为 r，宽度为 dr的细圆环，圆盘的质量面密度为2Rm，该圆环的元面积为rdrdS2，圆环的质量为drrdSdm2.该圆环对转轴的转动惯量为drrdmrdJ322则整个圆盘的转动惯量为221212240403mRRrdrrdJJRR 4.转轴沿圆筒几何轴的转动惯量)(222rRmJ.3在圆筒上取一微截圆筒，其质量为 dm ，再在该微截圆筒上取一宽度为 dr，半径为 r的元圆筒，记取得的元圆筒质量为 dM （由于微截圆筒和元圆筒的厚度非常微小，可将微截圆筒和元圆筒看成质量为 dm 和 dM 的圆环）.圆环的面密度)(22rRdm .元圆筒的面积rdrdS2元圆筒的质量rdrdSdM2元圆筒对 Z 轴的转动惯量为drrrrdrdJRrRr322)2())((21)(21212222444rRrRrRrRrdmrRrRrR2)()()(21222222则整个圆筒的转动惯量为)(2222022rRmdmrRdJJm.5.转轴沿圆柱体几何轴的转动惯量22mRJ .在圆柱体上取一微圆柱体，其质量为 dm ，由于该微圆柱体厚度极小，可将该微圆柱体看成一圆盘。在圆盘上取一宽度为 dr，半径为 r的圆环，记该圆环的质量为 dM 。圆盘的面密度为2Rdm.圆环的面积为rdrdS2，质量rdrdSdM2圆环的转动惯量drrdMrdJ32024圆盘的转动惯量为dmRRrdrrdJdJdJRRR22212240403000则整个圆柱体的转动惯量为22202mRdmRdJJm.6.转轴通过圆柱体中...