主成分分析和因子分析实例VIP免费

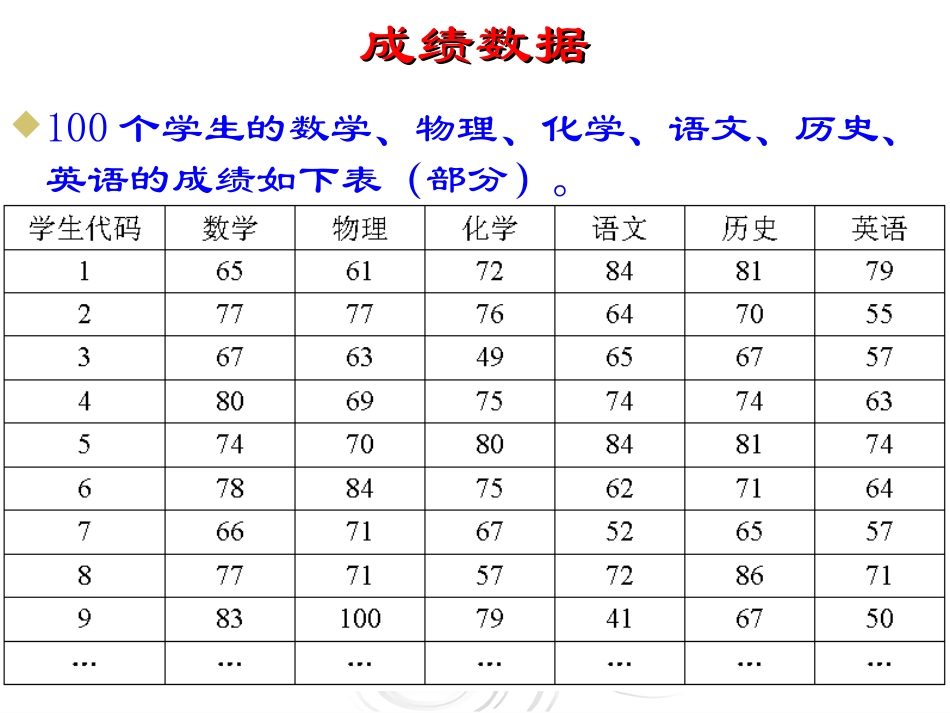
主成分与因子分析实例主成分与因子分析实例主成分分析和因子分析主成分分析和因子分析介绍两种把变量维数降低以便于描述、理解和分析的方法：主成分分析（principalcomponentanalysis）和因子分析（factoranalysis）。在引进主成分分析之前，先看下面的例子。成绩数据成绩数据100个学生的数学、物理、化学、语文、历史、英语的成绩如下表（部分）。从本例可能提出的问题从本例可能提出的问题目前的问题是，能不能把这个数据的6个变量用一两个综合变量来表示呢？这一两个综合变量包含有多少原来的信息呢？能不能利用找到的综合变量来对学生排序呢？这一类数据所涉及的问题可以推广到对企业、对学校进行分析、排序、判别和分类等问题。主成分分析主成分分析例中的数据点是六维的；也就是说，每个观测值是6维空间中的一个点。我们希望把6维空间用低维空间表示。先假定只有二维，即只有两个变量，它们由横坐标和纵坐标所代表；因此每个观测值都有相应于这两个坐标轴的两个坐标值；如果这些数据形成一个椭圆形状的点阵（这在变量的二维正态的假定下是可能的）主成分分析主成分分析那么这个椭圆有一个长轴和一个短轴。在短轴方向上，数据变化很少；在极端的情况，短轴如果退化成一点，那只有在长轴的方向才能够解释这些点的变化了；这样，由二维到一维的降维就自然完成了。主成分分析主成分分析当坐标轴和椭圆的长短轴平行，那么代表长轴的变量就描述了数据的主要变化，而代表短轴的变量就描述了数据的次要变化。但是，坐标轴通常并不和椭圆的长短轴平行。因此，需要寻找椭圆的长短轴，并进行变换，使得新变量和椭圆的长短轴平行。如果长轴变量代表了数据包含的大部分信息，就用该变量代替原先的两个变量（舍去次要的一维），降维就完成了。椭圆（球）的长短轴相差得越大降维也越有道理。主成分分析主成分分析对于多维变量的情况和二维类似，也有高维的椭球，只不过无法直观地看见罢了。首先把高维椭球的主轴找出来，再用代表大多数数据信息的最长的几个轴作为新变量；这样，主成分分析就基本完成了。注意，和二维情况类似，高维椭球的主轴也是互相垂直的。这些互相正交的新变量是原先变量的线性组合，叫做主成分(principalcomponent)。主成分分析主成分分析正如二维椭圆有两个主轴，三维椭球有三个主轴一样，有几个变量，就有几个主成分。选择越少的主成分，降维就越好。什么是标准呢？那就是这些被选的主成分所代表的主轴的长度之和占了主轴长度总和的大部分。有些文献建议，所选的主轴总长度占所有主轴长度之和的大约85%即可，其实，这只是一个大体的说法；具体选几个，要看实际情况而定。对于我们的数据，SPSS输出为：这里的InitialEigenvalues就是这里的六个主轴长度，又称特征值（数据相关阵的特征值）。TotalVarianceExplained3.73562.25462.2543.73562.25462.2541.13318.88781.1421.13318.88781.142.4577.61988.761.3235.37694.137.1993.32097.457.1532.543100.000Component123456Total%ofVarianceCumulative%Total%ofVarianceCumulative%InitialEigenvaluesExtractionSumsofSquaredLoadingsExtractionMethod:PrincipalComponentAnalysis.主成分分析的一般模型主成分分析的一般模型ppp2p21p1pp2p2221212p1p2121111xμxμxμYxμxμxμYxμxμxμYU组成的系数矩阵就是为系数μij1μμμ2kp2k22k1主成分分析主成分分析其中有以下原则来确定：ijμ第二大的的一切线一切线性组合xx是Y最大的的一切线一切线性组合xx是Y相互无关Y与Yp12p11ji这时称：Y1是第一主成分Y2是第二主成分主成分的含义主成分的含义由原始数据的协方差阵或相关系数据阵，可计算出矩阵的特征根：的方差对应的方差对应的方差对应则：pppYYY221121主成分的含义主成分的含义但是，spss软件中没有直接给出主成分系数，而是给出的因子载荷，我们可将因子载荷系数除以相应的，即可得到主成分系数。p12121111112111xppxxy合系数，即：为第一主成分的线性组，，...