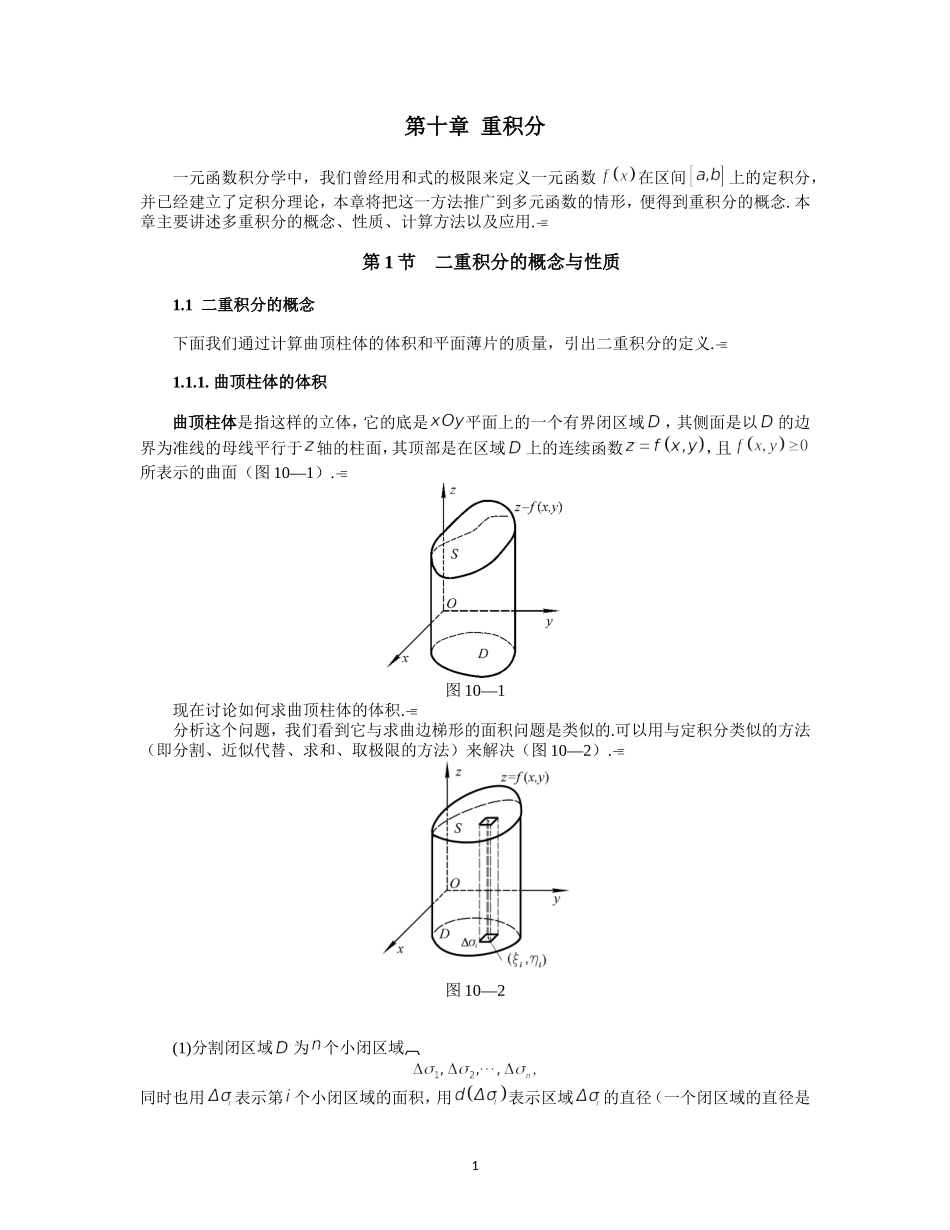
第十章重积分一元函数积分学中,我们曾经用和式的极限来定义一元函数在区间上的定积分,并已经建立了定积分理论,本章将把这一方法推广到多元函数的情形,便得到重积分的概念.本章主要讲述多重积分的概念、性质、计算方法以及应用.第1节二重积分的概念与性质1.1二重积分的概念下面我们通过计算曲顶柱体的体积和平面薄片的质量,引出二重积分的定义.1.1.1.曲顶柱体的体积曲顶柱体是指这样的立体,它的底是平面上的一个有界闭区域,其侧面是以的边界为准线的母线平行于轴的柱面,其顶部是在区域上的连续函数,且所表示的曲面(图10—1).图10—1现在讨论如何求曲顶柱体的体积.分析这个问题,我们看到它与求曲边梯形的面积问题是类似的.可以用与定积分类似的方法(即分割、近似代替、求和、取极限的方法)来解决(图10—2).图10—2(1)分割闭区域为个小闭区域同时也用表示第个小闭区域的面积,用表示区域的直径(一个闭区域的直径是1指闭区域上任意两点间距离的最大值),相应地此曲顶柱体被分为个小曲顶柱体.(2)在每个小闭区域上任取一点对第个小曲顶柱体的体积,用高为而底为的平顶柱体的体积来近似代替.(3)这个平顶柱体的体积之和就是曲顶柱体体积的近似值.(4)用表示个小闭区域的直径的最大值,即.当(可理解为收缩为一点)时,上述和式的极限,就是曲顶柱体的体积:1.1.2平面薄片的质量设薄片在平面占有平面闭区域,它在点处的面密度是.设且在上连续,求薄片的质量(见图10-3).图10-3先分割闭区域D为个小闭区域在每个小闭区域上任取一点近似地,以点处的面密度代替小闭区域上各点处的面密度,则得到第i块小薄片的质量的近似值为,于是整个薄片质量的近似值是用表示个小闭区域的直径的最大值,当无限细分,即当时,上述和式的极限就是薄片的质量,即.以上两个具体问题的实际意义虽然不同,但所求量都归结为同一形式的和的极限.抽象出来就得到下述二重积分的定义.定义1设是平面上的有界闭区域,二元函数在上有界.将分为个小区域同时用表示该小区域的面积,记的直径为,并令.2在上任取一点,作乘积并作和式.若时,的极限存在(它不依赖于的分法及点的取法),则称这个极限值为函数在上的二重积分,记作,即,(10-1-1)其中叫做积分区域,叫做被积函数,叫做面积元素,叫做被积表达式,与叫做积分变量,叫做积分和.在直角坐标系中,我们常用平行于轴和轴的直线(=常数和=常数)把区域分割成小矩形,它的边长是和,从而,因此在直角坐标系中的面积元素可写成,二重积分也可记作.有了二重积分的定义,前面的体积和质量都可以用二重积分来表示.曲顶柱体的体积V是函数在区域上的二重积分;薄片的质量是面密度在区域上的二重积分.因为总可以把被积函数看作空间的一曲面,所以当为正时,二重积分的几何意义就是曲顶柱体的体积;当为负时,柱体就在平面下方,二重积分就是曲顶柱体体积的负值.如果在某部分区域上是正的,而在其余的部分区域上是负的,那么在上的二重积分就等于这些部分区域上柱体体积的代数和.如果在区域上的二重积分存在(即和式的极限(10-1-1)存在),则称在上可积.什么样的函数是可积的呢?与一元函数定积分的情形一样,我们只叙述有关结论,而不作证明.如果是闭区域上连续,或分块连续的函数,则在上可积.我们总假定在闭区域上连续,所以在上的二重积分都是存在的,以后就不再一一加以说明.1.1.3二重积分的性质设二元函数在闭区域上连续,于是这些函数的二重积分存在.利用二重积分的定义,可以证明它的若干基本性质.下面列举这些性质.性质1常数因子可提到积分号外面.设是常数,则.性质2函数的代数和的积分等于各函数的积分的代数和,即3.性质3设闭区域被有限条曲线分为有限个部分闭区域,则上的二重积分等于各部分闭区域上的二重积分的和.例如分为区域和(见图10-4),则.(10-1-2)图10-4性质3表示二重积分对积分区域具有可加性.性质4设在闭区域上,为的面积,则.从几何意义上来看这是很明显的.因为高为1的平顶柱体的体积在数值上就等于柱体的底面积.性质5设在闭区域上有,则.由于又有.这就是说,函数二重积分的绝对值必小于或等于该函数绝对值的二重积...