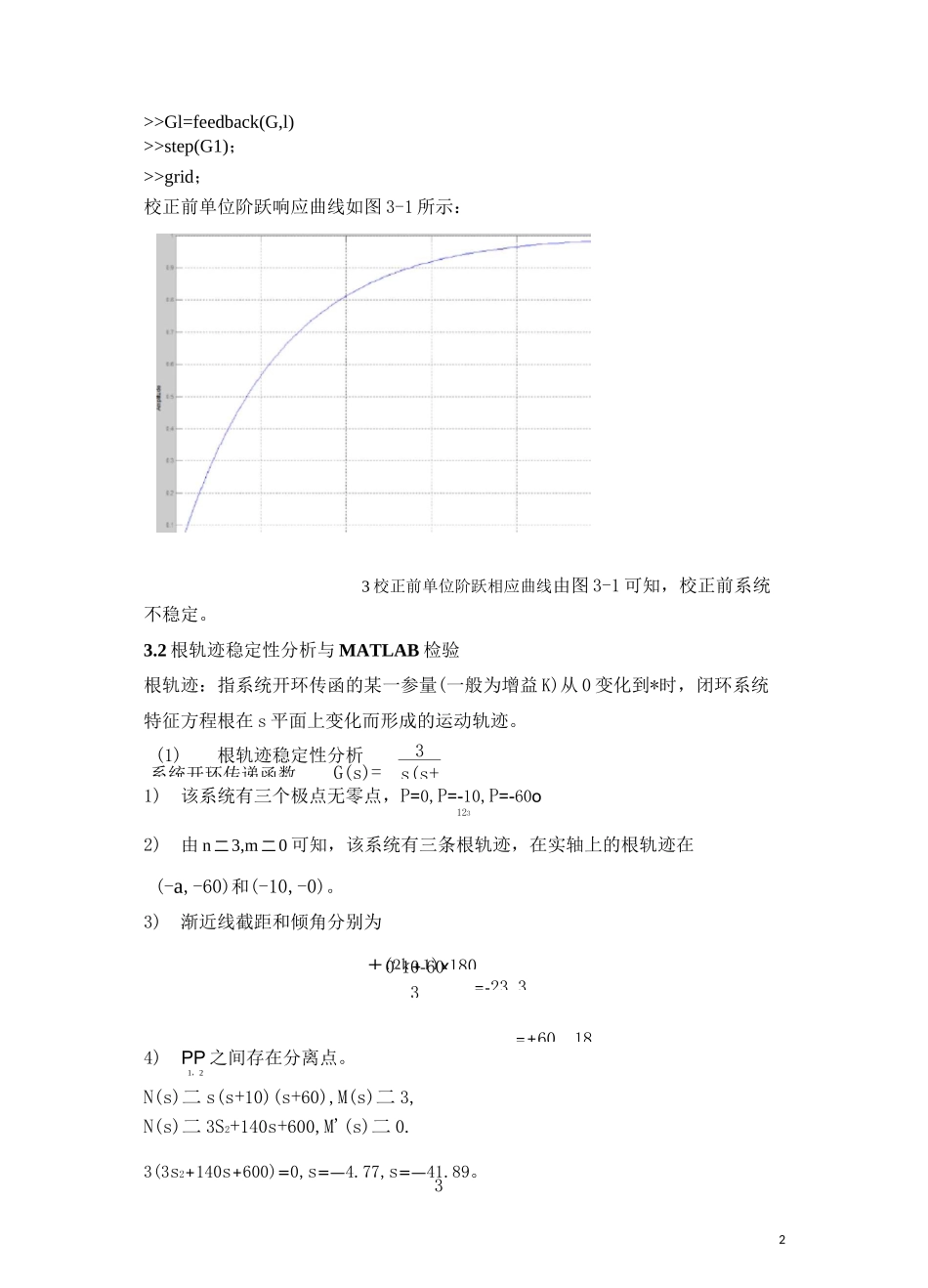
1设计要求:已知单位负反馈的开环传递函数为 G(s)二3s(s+10)(s+60)G(s)=k50s(s+1. 设计目的(1) 掌握线性系统的根轨迹、时域和频域分析与计算方法;(2) 掌握线性系统的超前、滞后、滞后-超前、一二阶最佳参数、PID 等校正方法;(3) 掌握 MATLAB 线性系统性能分析、校正设计与检验的基本方法2. 设计内容及要求设计内容:对所给系统进行基本性能指标计算、判断稳定性、根轨迹分析、时域和频域分析并对校正前后系统进行特性分析,完成对系统的校正设计。要求校正后系统的性能指标为:Y'〉45。,e<0.02。对于在设计中需要给出附加条件(如需要确定校正后的穿越频率 3'e 为速度误差精度等)时,应给出 css充分说明。首先,对给定的系统先进行时域指标分析、根轨迹稳定性分析、以及频域指标分析并进行 MATLAB 仿真效验。然后根据校正后的系统的性能指标对原系统进行校正,给出校正方案以及校正方案选择的理由、校正方案的思路及步骤。对校正后的系统再次进行时域指标分析、根轨迹稳定性分析、以及频域指标分析并进行 MATLAB 仿真校验。之后,进行校正前后系统性能指标的比较与分析。最后,实验总结,心得体会。3. 校正前系统分析1根据系统对稳定误差要求,该系统为 I 型系统,所以有 e=<0.02AK〉50,ssK令 K=50,因此,满足稳态误差要求的开环传递函数为3.1 时域性能指标计算与 MATLAB 检验单位阶跃响应程序如下所示:>>clear>>G=tf([50],[conv([1,10],[1,60]),0]);0-10-6033=-23.32土 (2 k + 1) x 180 。 =±60。,18系统开环传递函数G(s)=k3s(s+>>Gl=feedback(G,l)>>step(G1);>>grid;校正前单位阶跃响应曲线如图 3-1 所示:3 校正前单位阶跃相应曲线由图 3-1 可知,校正前系统不稳定。3.2 根轨迹稳定性分析与 MATLAB 检验根轨迹:指系统开环传函的某一参量(一般为增益 K)从 0 变化到*时,闭环系统特征方程根在 s 平面上变化而形成的运动轨迹。(1)根轨迹稳定性分析1)该系统有三个极点无零点,P=0,P=-10,P=-60o1232)由 n 二 3,m 二 0 可知,该系统有三条根轨迹,在实轴上的根轨迹在(-a,-60)和(-10,-0)。3)渐近线截距和倾角分别为4)PP 之间存在分离点。1,2N(s)二 s(s+10)(s+60),M(s)二 3,N(s)二 3S2+140s+600,M'(s)二 0.3(3s2+140s+600)=0,s=—4.77,s=—41.89。312则实轴根轨迹区间为(-e-60)和(-10,-0)。又因 s 不在根轨迹区间,因此不可能是分离点,分离点必落在 s 处。215) 根轨迹与实轴的虚...