球和多面体的切接关系讲解VIP免费

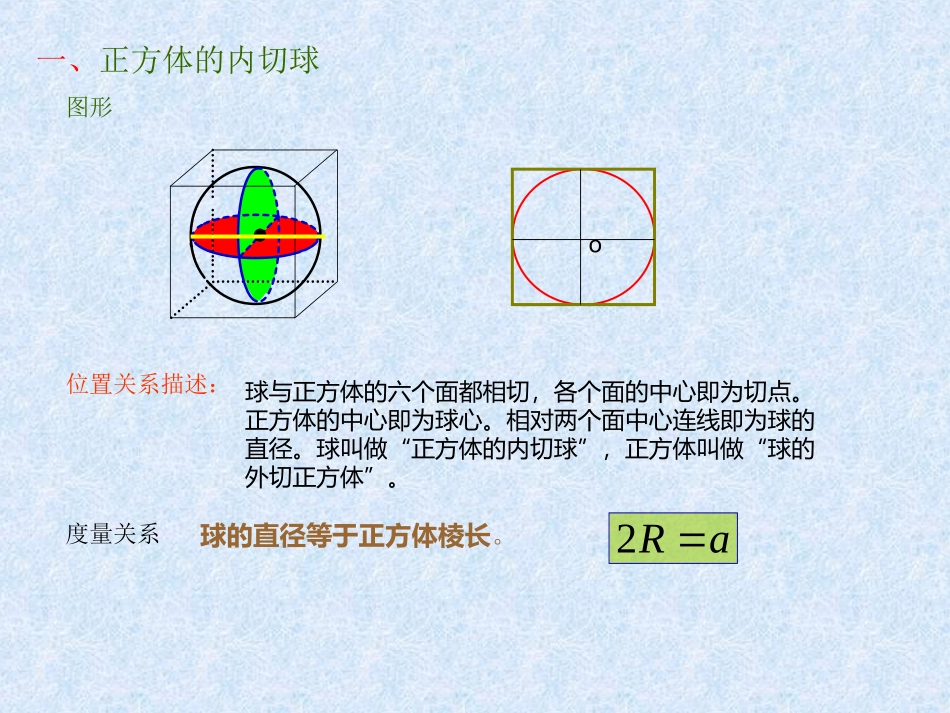
郸城一高数学组§1正方体与球动画显示一、正方体的内切球郸城一高高一数学组位置关系描述：球与正方体的六个面都相切，各个面的中心即为切点。正方体的中心即为球心。相对两个面中心连线即为球的直径。球叫做“正方体的内切球”，正方体叫做“球的外切正方体”。o图形度量关系球的直径等于正方体棱长。aR2一、正方体的内切球例题1求棱长为2的正方体的内切球的表面积解：因球与正方体内切，所以，球的直径等于正方体棱长，即441222rSrr即时练习：一个正方体的体积是8，则这个正方体的内切球的表面积是（）2.4.6.8.DCBAC动画显示二、球与正方体的棱相切位置关系描述：度量关系图形二、球与正方体的棱相切球与正方体的12条棱都相切，各棱的中点即为切点。正方体中心即为球心。“对棱”中点连线即为球的直径。球的直径等于正方体一个面上的对角线长aR22即时练习：在一个空的正方体框架内放置一球，若正方体棱长为a,则此球的最大体积是332a动画显示三、正方体的外接球图形位置关系描述：度量关系三、正方体的外接球正方体的8个顶点在同一个球面上。正方体的中心即为球心。球叫做“正方体的外接球”，正方体叫做“球的内接正方体”。正方体的（体）对角线等于球直径aR32____________课堂练习正方体的内切球与外接球半径的比是2:1.3:2.3:1.2:1.DCBAB正方体的全面积是，它的顶点都在球面上，则这个球的表面积是若球面内接正方体对角面面积为，设球面内接正方体的棱长为a，则对角面面积为124323,2,242222RSaRaaaa球的面积为球半径为2a22a24解：22222442662323,3266,6,aRSaaxRxRaxaxx球的表面积为得：由则设正方体的棱长为例题2求球的表面积§2长方体与球一、长方体的外接球位置关系描述：长方体的8个顶点在同一个球面上。长方体的中心（对角线的交点）即为球心。球叫做“长方体的外接球”，长方体叫做“球的内接长方体”。度量关系长方体的（体）对角线等于球直径图形Rcbalcba2222，则、、分别为设长方体的长、宽、高长方体一个顶点上三条棱的长分别为3、4、5，且它的八个顶点都在同一个球面上，那么，这个球的表面积是()200.50.225.220.DCBAC思考：一般的长方体有内切球吗？没有。一个球在长方体内部，最多可以和该长方体的5个面相切。如果一个长方体有内切球，那么它一定是正方体课堂练习例如，装乒乓球的盒子如图，半球内有一内接正方体，正方体的一个面在半球底面圆内。则这个半球的面积与正方体表面积的比为（）3.125.2.65.DCBAaaaal6)2(222将半球补成整球由长方体内接于球知：Rl2RaRa36,2629662622222RRaRSS正方体半球所以，选B分析1B例题3则两个同样的正方体对接构成的长方体就内接于这个球。设正方体棱长为a，则所得长方体对角线长为如图,半球内有一内接正方体，正方体的一个面在半球的底面圆内，若正方体的一边长为变式练习求半球的表面积和体积．答案：半球的表面积为27π，半球的体积为18π.6分析2aRRaaaABROBaOA26,22,,22222OABOAB设球心为O，则O亦为底面正方形的中心。26232622222aaaRSS正方体半球如图，连结OA、OB，则得RtΔOAB.设正方体棱长为a，易知：例题4在半径为R的球面上任取一点，过该点作两两互相垂直的三条弦，求证：这三条弦的平方和为定值。POABCDO1证明设过球O上一点P，作三条互相垂直的弦PA、PB、PC，如图所示设PB、PC所在的平面与球O相交于小圆⊙O1，因为PB与PC垂直，所以，BC为小圆⊙O1直径。连结PO1并延长交⊙O1于D，连结OO1.则OO1⊥平面⊙O1。易知PA⊥平面⊙O1，在小圆⊙O1中，2222PDBCPCPB2222)2(RADPDPA定值2222)2(RPCPBPA在大圆⊙O中，所以，OO1PA∥，所以球心O在A、P、D三点所确定的圆面内，即过A、P、D的圆面是球的大圆。又PAPD⊥，∴AD为该大圆的直径（即O为AD的中点）。点P在直径为的球面上，过P作两两互相垂直的三条弦（两端点均在球面上的线段），若其中一条弦长是另一条弦长的2倍，则这三条弦长之和的最大值是...