杆的纵向振动和轴的扭转振动VIP免费

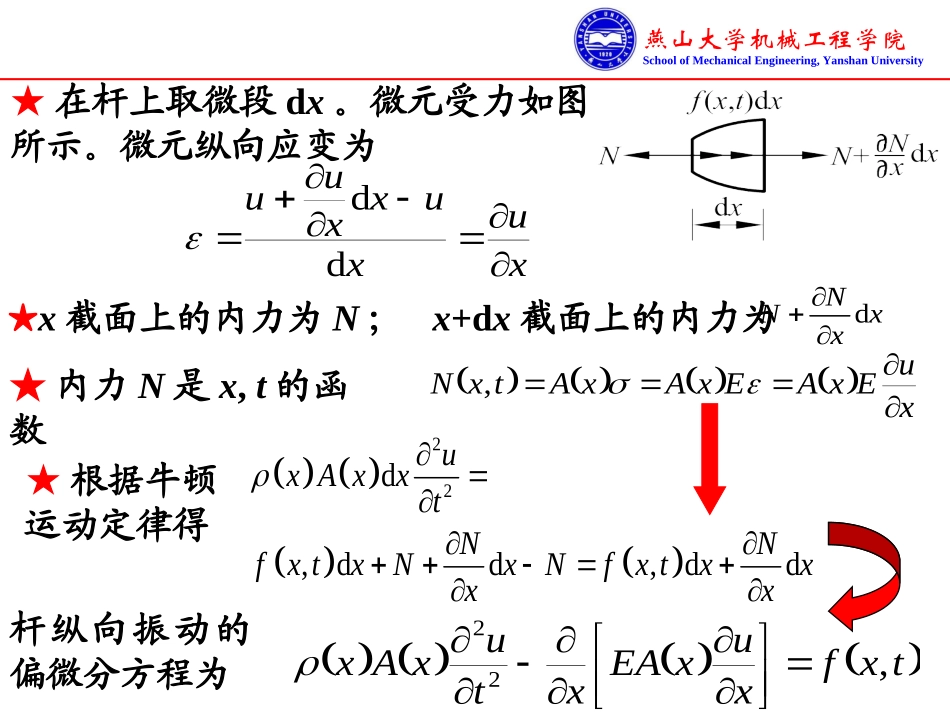
燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversity★假设:(1)杆的横截面在振动时始终保持为平面，并作整体运动；(2)略去杆纵向伸缩引起的横向变形。已知:(1)杆的单位体积的质量为(x)，截面积为A(x)，杆长为L，弹性模量为E；(2)杆受分布力f(x,t)作用作纵向振动。3.2杆的纵向振动坐标：以u(x,t)表示杆x截面在时刻t的位移，即位移是截面位置x和时间t的二元函数。燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversity★在杆上取微段dx。微元受力如图所示。微元纵向应变为ddxuxuxxuu★x截面上的内力为N；x+dx截面上的内力为dNNxxxuExAExAxAtxN,★内力N是x,t的函数★根据牛顿运动定律得22d,dd,dduxAxxtNNfxtxNxNfxtxxxx杆纵向振动的偏微分方程为txfxuxEAxtuxAx,22燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversity★若杆的单位体积质量(x)==常数，截面积A(x)=A=常数，杆纵向振动的偏微分方程简化为如果f(x,t)=0，则杆纵向自由振动的偏微分方程为22222uuatxa为弹性波沿x轴的传播速度。aEtxfxuxEAxtuxAx,22txfAxuEtu,12222燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversity类似于弦的横向振动，仍然采用分离变量法求解杆纵向振动的偏微分方程。设u(x，t)表示为tFxUtxu,22222uuatx0dd222tFttF222d00dUxUxxLxa杆纵向自由振动的偏微分方程可以分解为两个常微分方程燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversity式中：C,D为待定常数，由两个端点的边界条件决定。两个常微分方程的解0dd222tFttF222d00dUxUxxLxatBtAtFcossinxaDxaCxUcossin式中：A,B为待定常数，由两个初始条件决定。燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversity固有频率为1,2,rELrLarr振型函数为sin1,2,rrUxxrL边界条件对固有频率、振型的影响(1)两端固定固定端的变形必须为零，所以固定端的边界条件为00LUUxaDxaCxUcossin将边界条件代入振型函数00U0Dsin0CLa0ULD=0C=1燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversityC=0D=1固有频率为1,2,rELrLarr振型函数为cos1,2,rrUxxrL(2)两端自由0C自由端的应力为零，即应变为零，自由端的边界条件为0dddd0LxxxxUxxU0d0dxUxxd0dxLUxx=0，杆作刚体纵向平动0sin0Lasin0DLaasincoscossinUxCxDxaadUxCxDxdxaaaa燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversityD=0C=1(3)一端固定一端自由的杆边界条件为00d0dxLUUxx由此得0D0cosLaaC频率方程为0cosLa固有频率为21211,2,22rrarErLL振型函数为sincos21sin1,2,2rrrUxCxDxaarxrLsincoscossinUxCxDxaadUxCxDxdxaaaa燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversity对于上述三种边界条件：两端固定的杆；两端自由的杆；一端固定、一端自由的杆。前三阶振型图为：燕山大学机械工程学院SchoolofMechanicalEngineering,YanshanUniversity解：上端固定的边界条件为000,0Utu或下端具有附加质量M，在振动时产生对杆端的惯性力。取质块为研究对象，杆对质块的作用力方向向上，下端点的边界条件为22,,ttLuMxtLuEA例-1求如图所示...