多面体和球的接切问题VIP免费

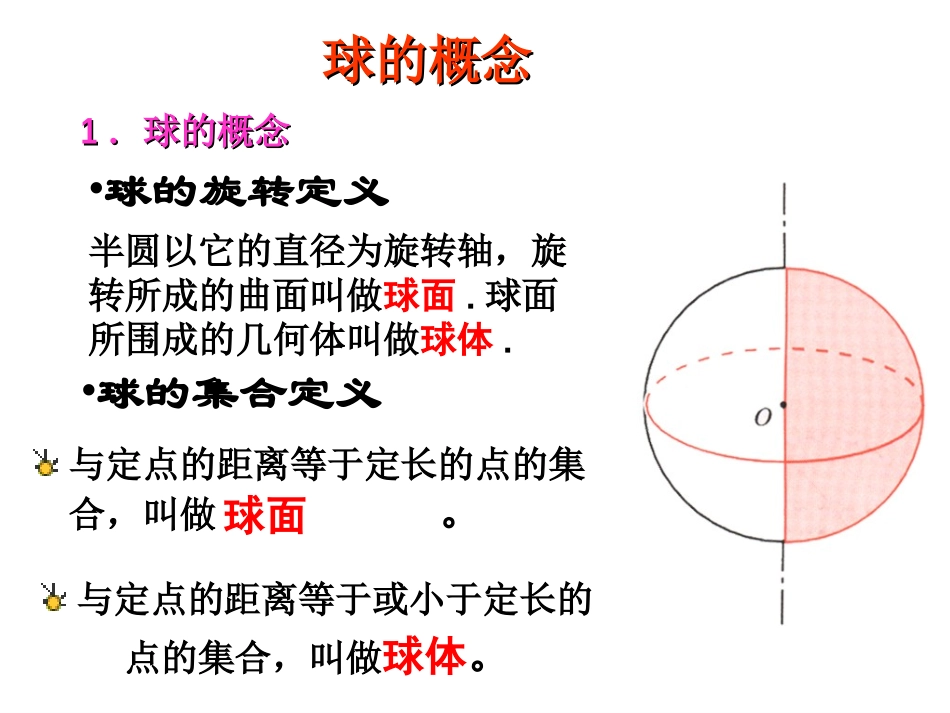
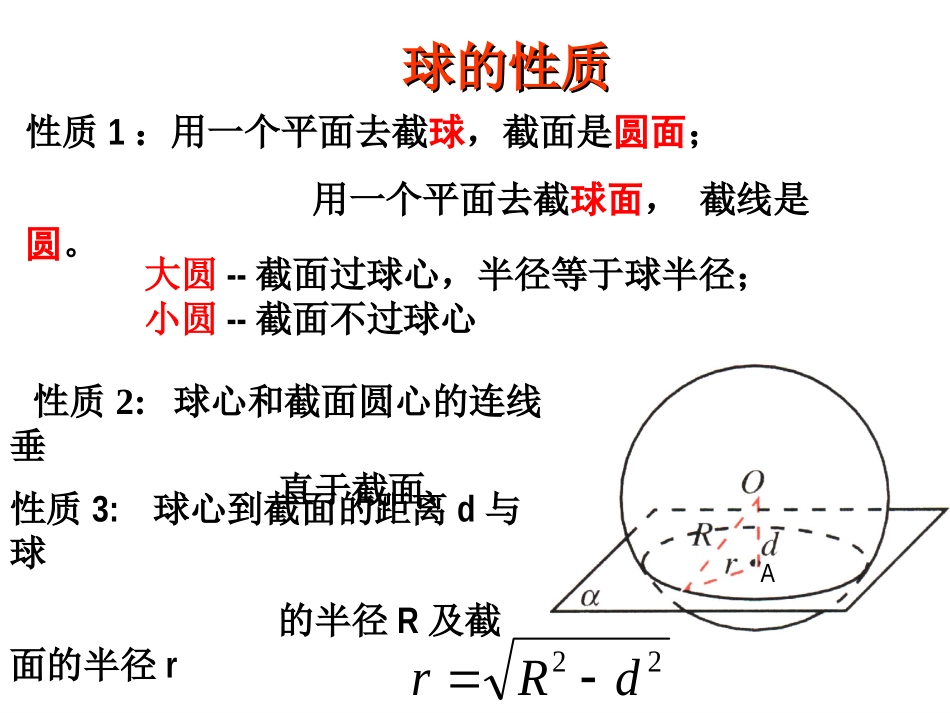
简单多面体与球的接切问题球的概念球的概念11．球的概念．球的概念与定点的距离等于定长的点的集合，叫做。半圆以它的直径为旋转轴，旋转所成的曲面叫做球面.球面所围成的几何体叫做球体.•球的旋转定义•球的集合定义与定点的距离等于或小于定长的点的集合，叫做球体。球面球的性质球的性质性质2:球心和截面圆心的连线垂直于截面．22dRr性质1：用一个平面去截球，截面是圆面；用一个平面去截球面，截线是圆。大圆--截面过球心，半径等于球半径；小圆--截面不过球心性质3:球心到截面的距离d与球的半径R及截面的半径r有下面的关系:A一球的球面面积为256πcm2，过此球的一条半径中点，作垂直于这条半径的截面，求截面圆的半径和面积．解：设O为球心，O′为截面圆圆心，如右图，则OO′⊥O′A，O′A为截面圆半径，OA为球的半径．根据球的表面积公式，则有：4π·AO2＝256π，得AO＝8cm，在Rt△AO′O中，OO′＝12AO＝4cm.所以AO′＝AO2－OO′2＝82－42＝43(cm)．S截面圆＝π·AO′2＝π·(43)2＝48π(cm2)．所以截面圆半径为43cm，面积为48πcm2.31.3ara结论：边长为的正三角形的外接圆半径2.2ccr斜边为的直角三角形的外接圆半径223.2ababr长为，宽为的矩形的外接圆半径正方体的内切球,外接球,棱切球§正方体与球切点：各个面的中心。球心：正方体的中心。直径：相对两个面中心连线。o球的直径等于正方体棱长。aR2一、正方体的内切球二、球与正方体的棱相切球的直径等于正方体一个面上的对角线长aR22切点：各棱的中点。球心：正方体的中心。直径：“对棱”中点连线三、正方体的外接球球直径等于正方体的（体）对角线aR32正方体的内切球,棱切球,外接球三个球心合一1:2:3半径之比为：§长方体与球一、长方体的外接球长方体的（体）对角线等于球直径Rcbalcba2222，则、、分别为设长方体的长、宽、高一般的长方体有内切球吗？没有。一个球在长方体内部，最多可以和该长方体的5个面相切。如果一个长方体有内切球，那么它一定是正方体？例：例：如图，半球内有一内接正方体，正方体的一个面在半球底面圆内。则这个半球的面积与正方体表面积的比为（）将半球补成整球aaaal6)2(222分析2222222,,22,232OAaOBRABaaaRRaOABOAB设球心为O，则O亦为底面正方形的中心。如图，连结OA、OB，则得RtΔOAB.设正方体棱长为a，易知：222223662SRaSaa半球正方体例.已知球O的表面上有P、A、B、C四点，且PA、PB、PC两两互相垂直，若PA=PB=PC=a，求这个球的表面积和体积。变式：将上面的条件改为“PA=a,PB=b,PC=c”3VS表表内切球半径公式：r=，其中V为几何体的体积，S为几何体的表面积例：如图为某几何体的三视图，该几何体的内切球体积为______334221=34=12311=3+342+352=36223==1VSVS四棱锥表表内切球半径r§正四面体与球1.棱长为a的正四面体的外接球的半径为___PABCMORR.正四面体的外接球可利用直角三角形勾股定理来求DPADOME226.4Ra将正四面体放到正方体中，得正方体的棱长为a,且正四面体的外接球即正方体的外接球，所以＝2.棱长为a的正四面体的棱切球的半径_____24Ra＝3.棱长为a的正四面体的内切球的半径_____rShSV全面积底面积3131ar126ShSr底面积全面积14SrSh底面积全面积14rh？63haOPABCDKH正四面体的内切球还可利用截面三角形来求ABEOO1Far126内切64Ra外接＝24Ra棱切＝正四面体的内切球,棱切球,外接球3:1:33半径之比为：正四面体的四条高相交于同一点，这点叫做正四面体的中心。正四面体的外接球、内切球是同心球，球心即为正四面体的中心。正四面体常常补成正方体求外接球的半径三条侧棱两两垂直的三棱锥常补成长方体小结:常见的补形OPABCDHMOHPABCDM球心在高PH上，即在锥体内部球心在高PH的延长线上，即在锥体外部球心与底面正Δ中心H重合OPACDMHB§正三棱锥与球正三棱锥的外接球的球心在它的高所在直线上度量关系：设正三棱锥底面边长为b，侧棱长为a，高为h，外接圆半径为R，222)33(hbaRhaPMPHPA2,22即或在RtΔAHO中，222222)()33,RRhbAOHOAH...