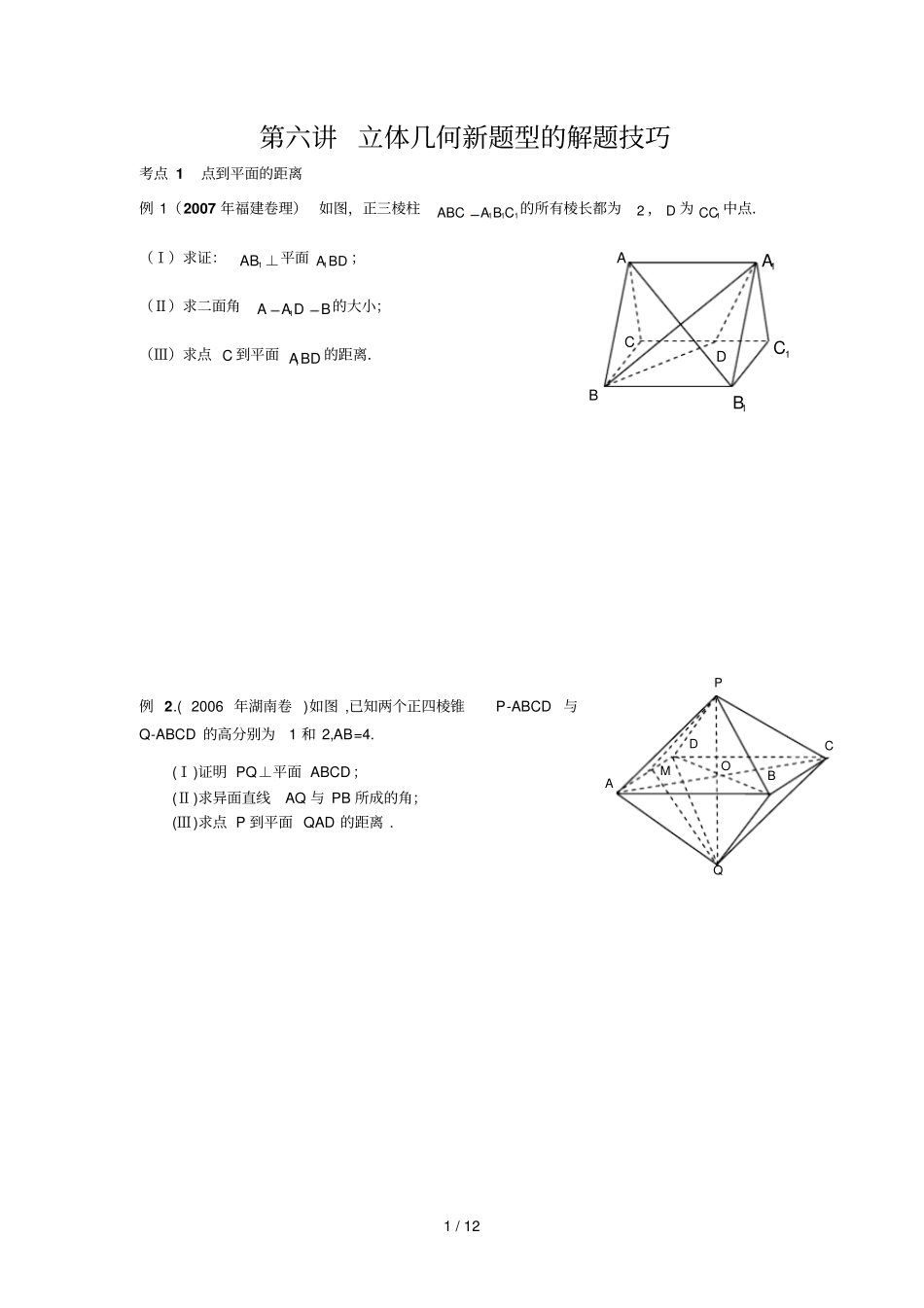
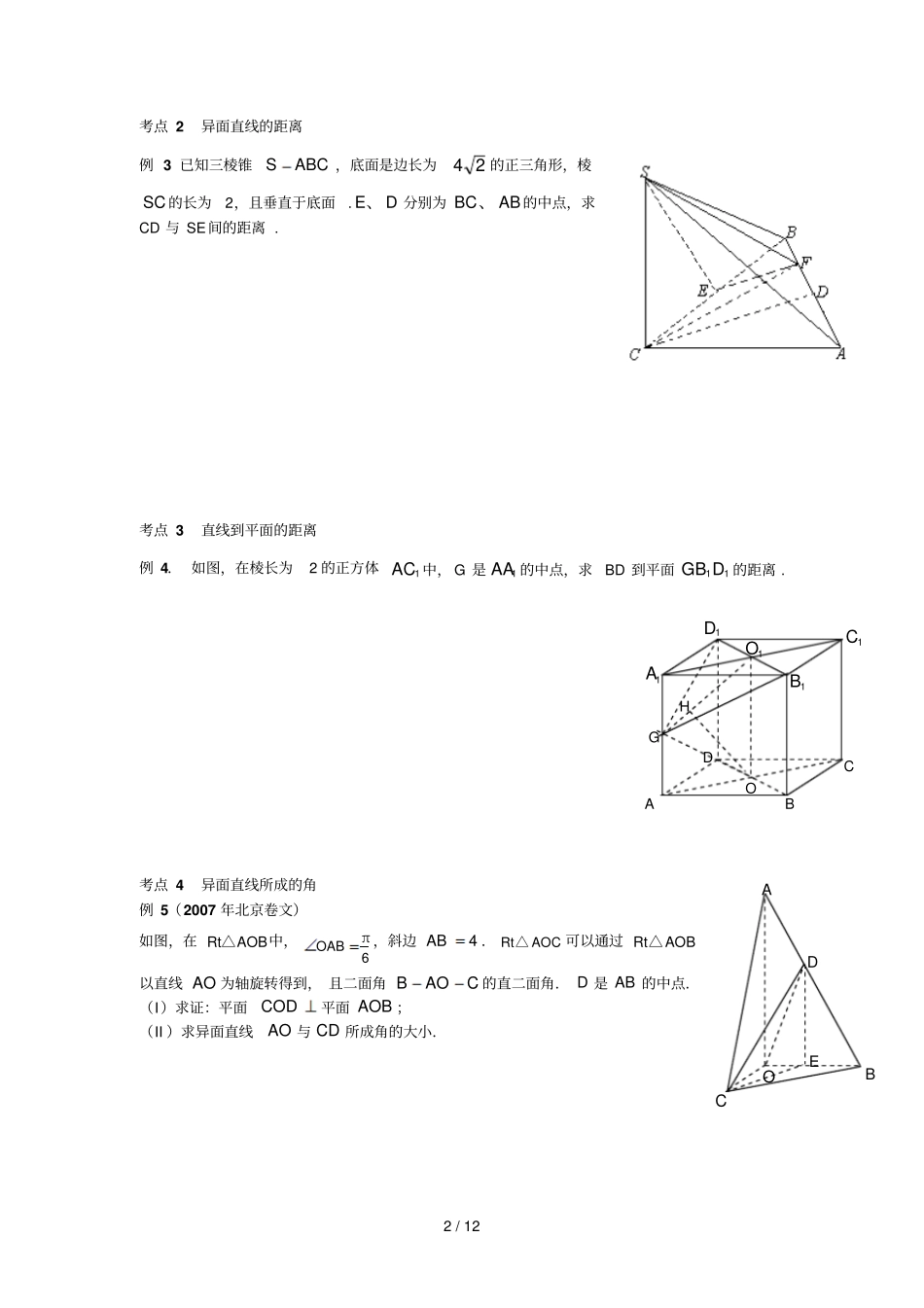
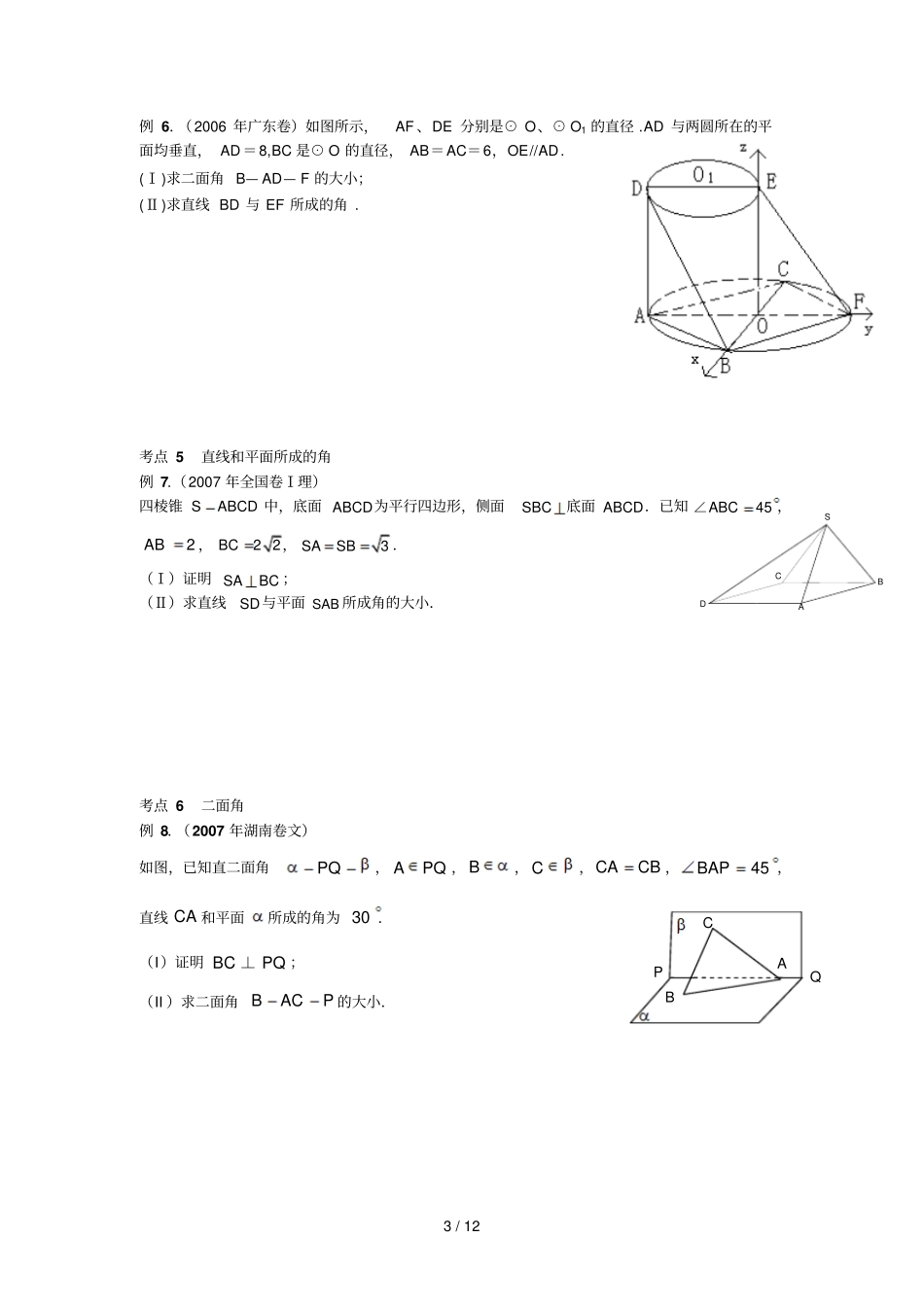
1 / 12 第六讲 立体几何新题型的解题技巧考点 1 点到平面的距离例 1(2007 年福建卷理) 如图,正三棱柱111ABCA B C 的所有棱长都为2 , D 为1CC 中点.(Ⅰ)求证:1AB ⊥平面1A BD ;(Ⅱ)求二面角1AA DB的大小;(Ⅲ)求点 C 到平面1ABD 的距离.例 2.( 2006 年湖南卷 )如图 ,已知两个正四棱锥P-ABCD与Q-ABCD 的高分别为1 和 2,AB=4. (Ⅰ)证明 PQ⊥平面 ABCD ;(Ⅱ)求异面直线AQ 与 PB 所成的角;(Ⅲ)求点 P 到平面 QAD 的距离 . Q B C P A D O M A B C D 1A1C1B2 / 12 考点 2 异面直线的距离例 3 已知三棱锥ABCS,底面是边长为24的正三角形,棱SC 的长为2,且垂直于底面.DE、分别为ABBC、的中点,求CD 与 SE间的距离 . 考点 3 直线到平面的距离例 4. 如图,在棱长为2 的正方体1AC 中, G 是1AA 的中点,求BD 到平面11DGB的距离 . 考点 4 异面直线所成的角例 5(2007 年北京卷文)如图,在 RtAOB△中,π6OAB,斜边4AB. RtAOC△可以通过 RtAOB△以直线 AO 为轴旋转得到, 且二面角 BAOC 的直二面角. D 是 AB 的中点.(I)求证:平面COD平面 AOB ;(II )求异面直线AO 与 CD 所成角的大小.B A C D O G H 1A1C1D1B1OOCADBE3 / 12 A B C Q P 例 6.(2006 年广东卷)如图所示,AF 、DE 分别是⊙ O、⊙ O1 的直径 .AD 与两圆所在的平面均垂直, AD=8,BC 是⊙ O 的直径, AB=AC=6,OE//AD. (Ⅰ)求二面角 B— AD— F 的大小;(Ⅱ)求直线 BD 与 EF 所成的角 . 考点 5 直线和平面所成的角例 7.(2007 年全国卷Ⅰ理)四棱锥 SABCD 中,底面 ABCD为平行四边形,侧面SBC底面 ABCD.已知45ABC∠,2AB,2 2BC,3SASB.(Ⅰ)证明 SABC ;(Ⅱ)求直线SD与平面 SAB 所成角的大小.考点 6 二面角例 8.(2007 年湖南卷文)如图,已知直二面角PQ, APQ , B, C,CACB ,45BAP,直线 CA 和平面所成的角为 30 .(I)证明 BCPQ⊥;(II )求二面角 BACP 的大小.DBCAS4 / 12 例 9.( 2006 年重庆卷 )如图,在四棱锥P-ABCD 中, PA底面ABCD ,DAB 为直角, AB‖CD,AD=CD=2AB, E、F 分别为 PC、CD 的中点 . (Ⅰ)试证: CD平面 BEF;(Ⅱ)设 PA=k· AB,且二面角 E-BD-C 的平面角大于30 ,求 k 的取值范围 . 考点 7 利用空间向量求空...