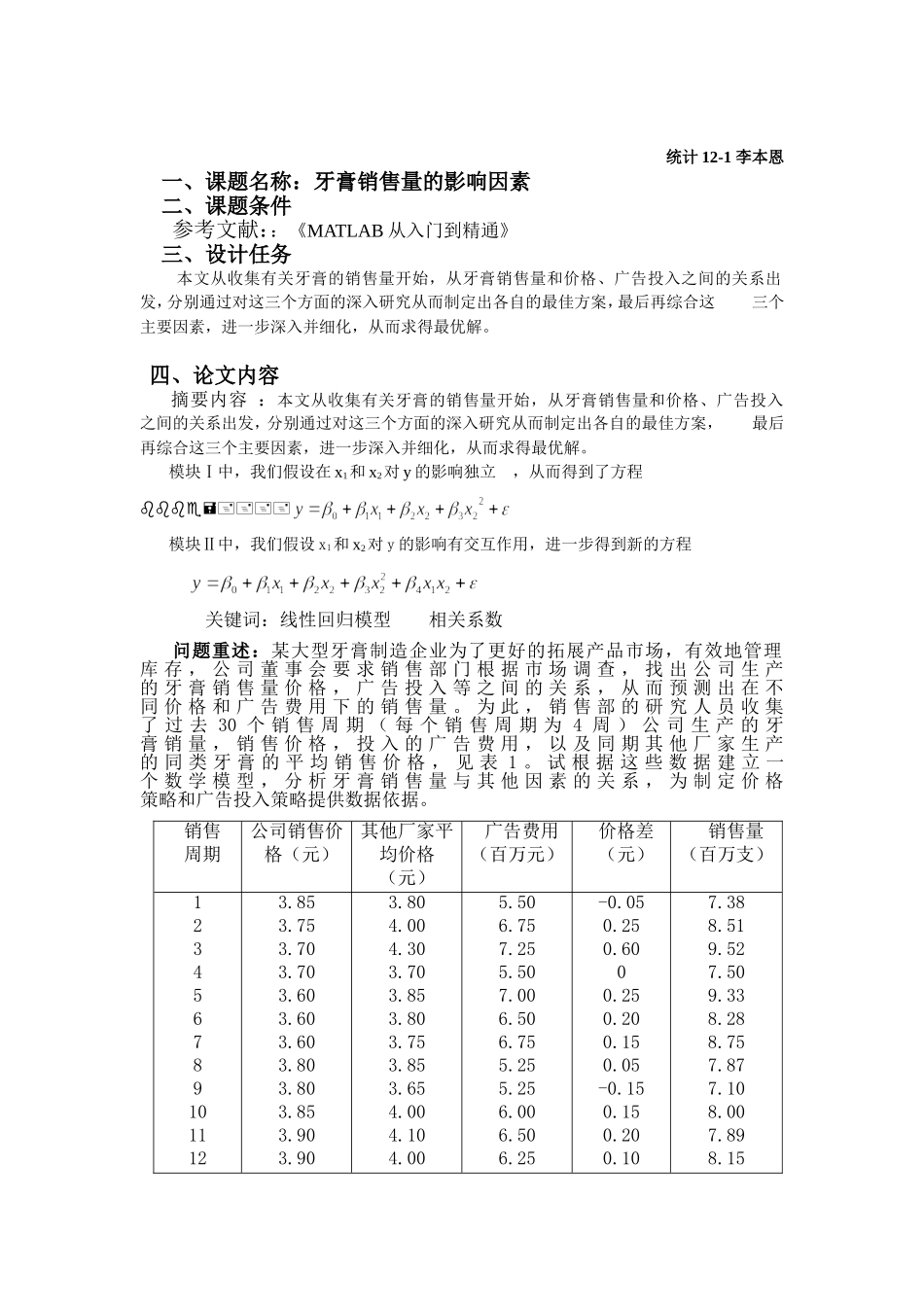
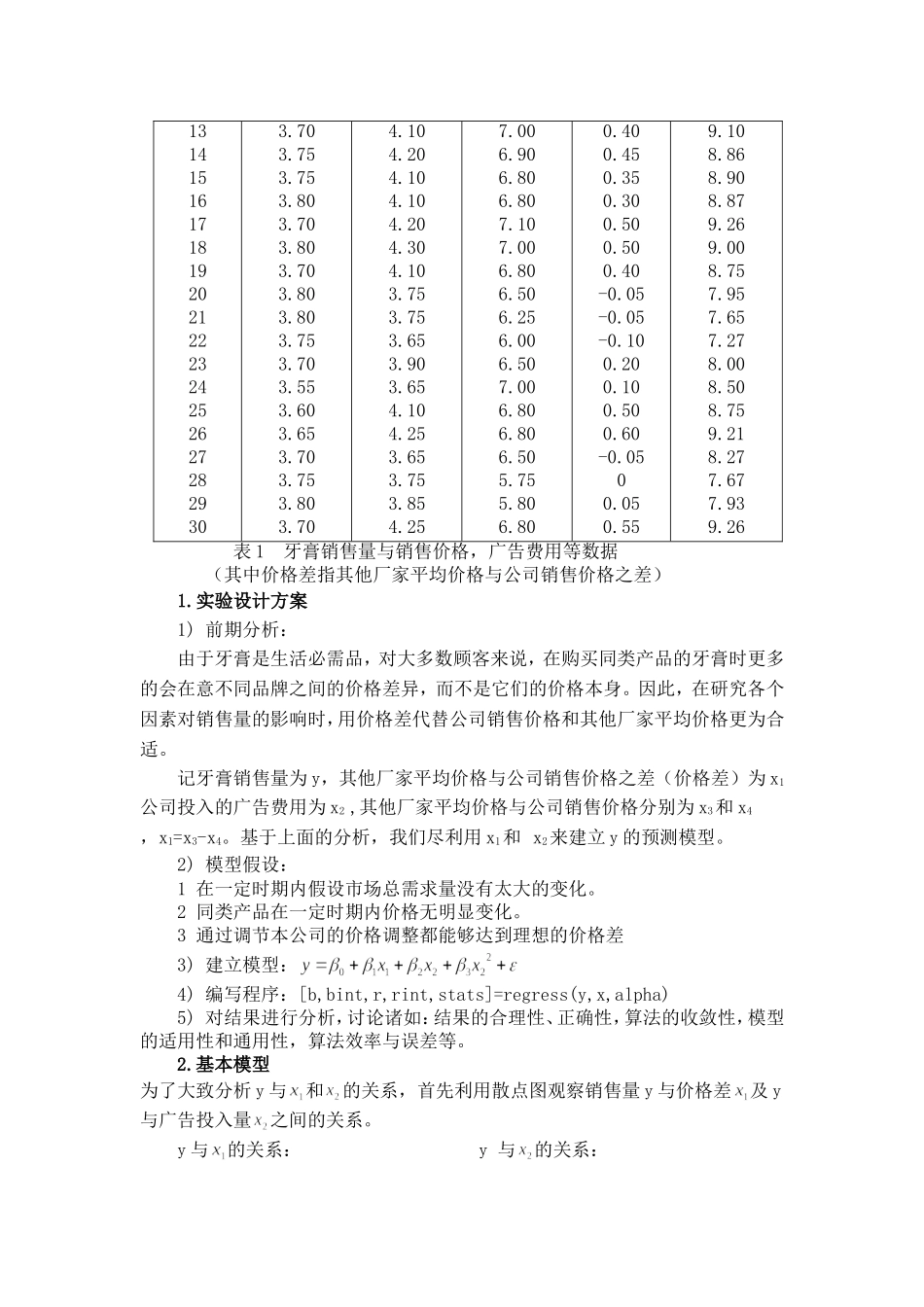
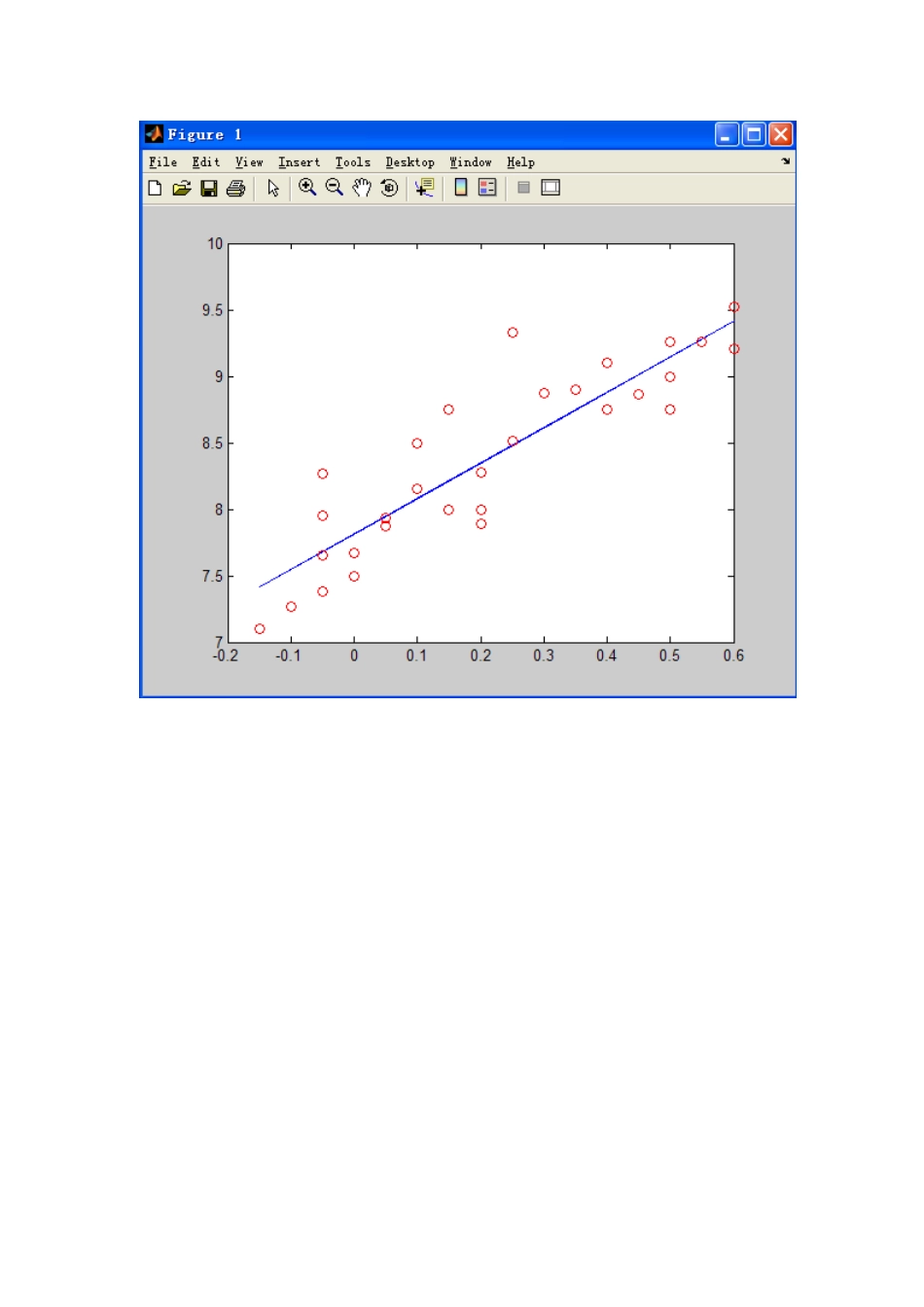
统计12-1李本恩一、课题名称:牙膏销售量的影响因素二、课题条件参考文献::《MATLAB从入门到精通》三、设计任务本文从收集有关牙膏的销售量开始,从牙膏销售量和价格、广告投入之间的关系出发,分别通过对这三个方面的深入研究从而制定出各自的最佳方案,最后再综合这三个主要因素,进一步深入并细化,从而求得最优解。四、论文内容摘要内容:本文从收集有关牙膏的销售量开始,从牙膏销售量和价格、广告投入之间的关系出发,分别通过对这三个方面的深入研究从而制定出各自的最佳方案,最后再综合这三个主要因素,进一步深入并细化,从而求得最优解。模块Ⅰ中,我们假设在x1和x2对y的影响独立,从而得到了方程模块Ⅱ中,我们假设x1和x2对y的影响有交互作用,进一步得到新的方程关键词:线性回归模型相关系数问题重述:某大型牙膏制造企业为了更好的拓展产品市场,有效地管理库存,公司董事会要求销售部门根据市场调查,找出公司生产的牙膏销售量价格,广告投入等之间的关系,从而预测出在不同价格和广告费用下的销售量。为此,销售部的研究人员收集了过去30个销售周期(每个销售周期为4周)公司生产的牙膏销量,销售价格,投入的广告费用,以及同期其他厂家生产的同类牙膏的平均销售价格,见表1。试根据这些数据建立一个数学模型,分析牙膏销售量与其他因素的关系,为制定价格策略和广告投入策略提供数据依据。销售周期公司销售价格(元)其他厂家平均价格(元)广告费用(百万元)价格差(元)销售量(百万支)1234567891011123.853.753.703.703.603.603.603.803.803.853.903.903.804.004.303.703.853.803.753.853.654.004.104.005.506.757.255.507.006.506.755.255.256.006.506.25-0.050.250.6000.250.200.150.05-0.150.150.200.107.388.519.527.509.338.288.757.877.108.007.898.151314151617181920212223242526272829303.703.753.753.803.703.803.703.803.803.753.703.553.603.653.703.753.803.704.104.204.104.104.204.304.103.753.753.653.903.654.104.253.653.753.854.257.006.906.806.807.107.006.806.506.256.006.507.006.806.806.505.755.806.800.400.450.350.300.500.500.40-0.05-0.05-0.100.200.100.500.60-0.0500.050.559.108.868.908.879.269.008.757.957.657.278.008.508.759.218.277.677.939.26表1牙膏销售量与销售价格,广告费用等数据(其中价格差指其他厂家平均价格与公司销售价格之差)1.实验设计方案1)前期分析:由于牙膏是生活必需品,对大多数顾客来说,在购买同类产品的牙膏时更多的会在意不同品牌之间的价格差异,而不是它们的价格本身。因此,在研究各个因素对销售量的影响时,用价格差代替公司销售价格和其他厂家平均价格更为合适。记牙膏销售量为y,其他厂家平均价格与公司销售价格之差(价格差)为x1公司投入的广告费用为x2,其他厂家平均价格与公司销售价格分别为x3和x4,x1=x3-x4。基于上面的分析,我们尽利用x1和x2来建立y的预测模型。2)模型假设:1在一定时期内假设市场总需求量没有太大的变化。2同类产品在一定时期内价格无明显变化。3通过调节本公司的价格调整都能够达到理想的价格差3)建立模型:4)编写程序:[b,bint,r,rint,stats]=regress(y,x,alpha)5)对结果进行分析,讨论诸如:结果的合理性、正确性,算法的收敛性,模型的适用性和通用性,算法效率与误差等。2.基本模型为了大致分析y与和的关系,首先利用散点图观察销售量y与价格差及y与广告投入量之间的关系。y与的关系:y与的关系:图1y对散点图(1)图2y对的散点图从图(1)发现,随着增加,y的值有明显的线性增加趋势,图中直线用线性模型(1)拟合的(其中是随机误差)在图2中,当增大时,y有向上弯曲增加的趋势,图中的曲线用二次函数模型:(2)拟合。综上分析,结合模型(1)和(2)建立如下回归模型(3)其中,y是建立的模型,我们用对y进行估计,其中是我们待估计的参数。3.模型求解利用MATLAB统计工具箱中的命令regress求解,使用格式为:[b,bint,r,rint,stats]=regress(y,x,alpha)得到模型(3)的回归系数的估计值及其置信区间(置信水平)、检验统计量,S2的结果...