点到平面的距离VIP免费

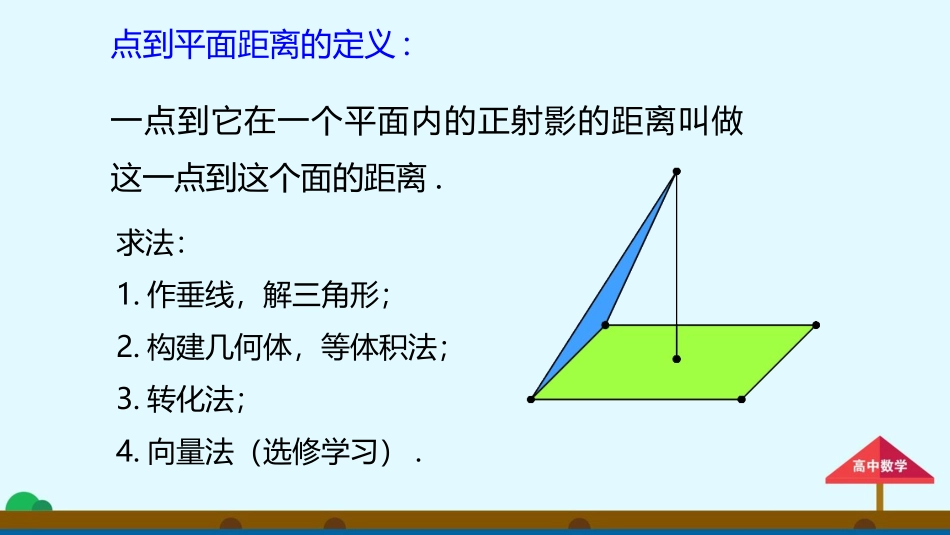
点到平面的距离看这个几何模型，我们要求它的体积，很多时候底面积很简单，关键是几何体的高，也就是顶点到底面的距离，这个距离就是点面距.HEABCO点到平面距离的定义:一点到它在一个平面内的正射影的距离叫做这一点到这个面的距离.求法：1.作垂线，解三角形；2.构建几何体，等体积法；3.转化法；4.向量法（选修学习）.解：连接AC.因为PA⊥平面ABCD，所以PA⊥CF.又CF⊥PC，PA∩PC=P，所以CF⊥平面PAC，所以平面PFC⊥平面PAC.过点A作AH⊥PC于H，所以AH⊥平面PCF，即AH为点A到平面PCF的距离.由已知AB=BC=1，所以AC=,PC=.在Rt△PAC中，得AH=.2363规律小结求点到面的距离步骤：1、找.找面的垂线；2、证.证明线是垂线；3、计算.运用解三角形计算.如图，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.(1)证明：BC⊥PD；(2)求点C到平面PDA的距离．(1)证明：因为BC⊥CD，平面PDC⊥平面ABCD，且平面PDC∩平面ABCD＝CD，BC⊂平面ABCD，所以BC⊥平面PDC.因为PD⊂平面PDC，所以BC⊥PD.(2)解：取CD的中点E，连接PE，AC．因为PD＝PC，所以PE⊥CD，所以PE＝PCCE22＝2243＝7.因为平面PDC⊥平面ABCD且平面PDC∩平面ABCD＝CD，PE⊂平面PDC，所以PE⊥平面ABCD.由(1)知BC⊥平面PDC.又AD∥BC，所以AD⊥平面PDC.又PD⊂平面PDC，所以AD⊥PD.设点C到平面PDA的距离为h，则VCPDA＝VPACD，所以13S△PDA·h＝13S△ACD·PE，所以h＝S△ACD·PES△PDA＝12×3×6×712×3×4＝372，已知正三角形△ABC的边长为6cm，点O到△ABC各顶点的距离都是4cm，求点O到这个三角形所在平面的距离.解：设H为点O在平面ABC内的射影，延长AH，交BC于E，则OAOBOCHAHBHC即H是△ABC的外心.在Rt△OHC中，132CEBC23cos30CECH22224(23)2(cm)OHOBBH即点O到这个三角形所在平面的距离为2cm.HEABCO