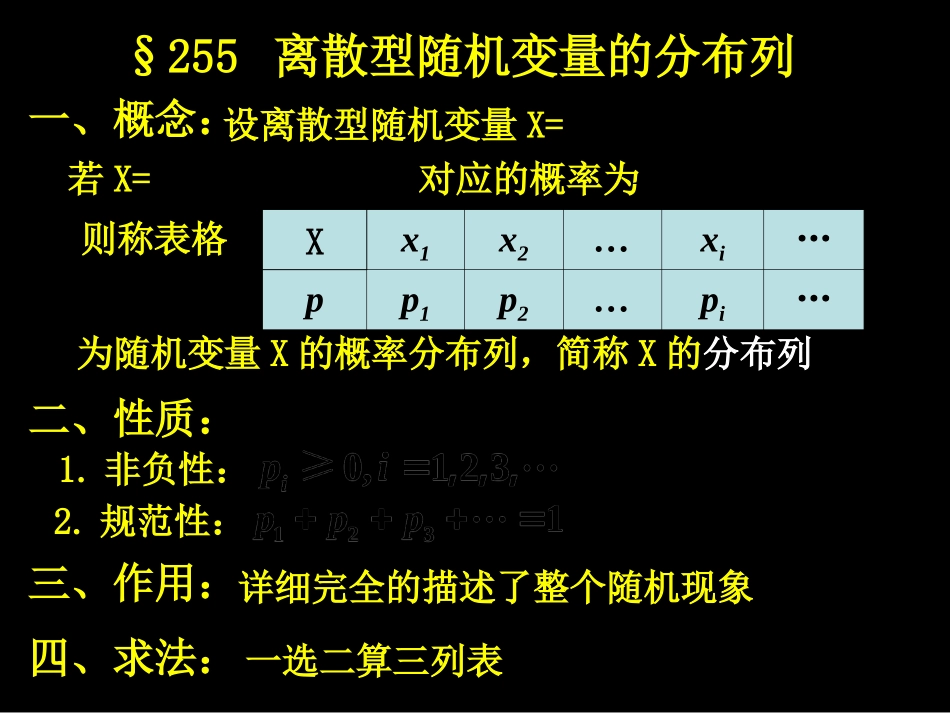
若X=对应的概率为123,,,,ixxxx为随机变量X的概率分布列,简称X的分布列则称表格(1,2,)ixi()iiPxp设离散型随机变量X=Xx1x2…xi…pp1p2…pi…§255离散型随机变量的分布列一、概念:二、性质:四、求法:三、作用:1.非负性:2.规范性:一选二算三列表详细完全的描述了整个随机现象随机事件分布列每种结果是否发生的用概率来衡量期望方差确定化④细化数化分布列①六大分布公式化③一选二算三列表②注①:细化数化分布列将随机试验的每种结果用变量(随机变量)来表示(1)细化:繁(大)事件(2)数化:(3)分布列:将每个随机变量及其所对应的概率列成表格简(小)事件分类:互斥事件加法公式分步:独立事件乘法公式随机变量及其分布列概述随机事件分布列期望方差确定化④细化数化分布列①六大分布公式化③一选二算三列表②注②:一选二算三列表求分布列的操作步骤注③:六大分布公式化(1)均匀分布(2)两点(0—1)分布(3)几何分布(4)超几何分布(5)二项分布(6)正态分布随机变量及其分布列概述随机事件分布列期望方差确定化④细化数化分布列①六大分布公式化③一选二算三列表②注④:期望方差确定化(1)期望:(2)方差:将随机事件“虚拟”成一确定事件体现了总体的平均水平(聚中性)体现了总体的稳定性(波动性)随机变量及其分布列概述注:互斥、对立及独立间的关联:不能同时为互斥互斥特例为对立互不影响为独立一对独立全独立互斥独立不相干概率相等即重复ΩΩA3A1A2……AA事件间的关系③和(并)④积(交)①包含(子事件)②相等⑦独立⑤互斥⑥对立⑧容斥③④①A+B=A∪B②AB=A∩B⑤=AB+ABA·BA·B=A+BA+B=A·B·CA+B+CA·B·C=A+B+CA、B中至少有一个发生A、B要同时发生A、B中恰好有一个发生A、B都不发生A、B不都发生A、B、C都不发生A、B、C不都发生常见事件的字母表示若X=对应的概率为123,,,,ixxxx为随机变量X的概率分布列,简称X的分布列则称表格(1,2,)ixi()iiPxp设离散型随机变量X=Xx1x2…xi…pp1p2…pi…§255离散型随机变量的分布列一、概念:二、性质:四、求法:三、作用:1.非负性:2.规范性:一选二算三列表详细完全的描述了整个随机现象若X=对应的概率为123,,,,ixxxx为随机变量X的概率分布列,简称X的分布列则称表格(1,2,)ixi()iiPxp设离散型随机变量X=Xx1x2…xi…pp1p2…pi…一、概念:注:视随机变量X为自变量,对应的概率P(x)为因变量一般的,不做说明时,X的分布列,特指表格则解析式,表格或图像均为X的分布列()iiPxp二、性质:1.非负性:2.规范性:练习1.概念与性质(1)课本P:49A组Ex4(2)设X是一个随机变量,其概率分布列是则q=______2112qq1,2()222析:由分布列的性质得(舍“+”)即2q2-4q+1=0,解得故q=222q三、作用:详细完全的描述了整个随机现象练习2.作用(3)课本P:49A组Ex5解:由题意得)8(Xp)10()9()8(XpXpXp79.022.029.028.0故所求概率为0.79四、求法:一选二算三列表一选:根据题意灵活的选取随机变量所有可能的取值二算:根据题意灵活的计算各随机变量相应的概率化繁为简以小代大定义法复杂事件的概率简单事件的概率模拟试验法性质公式法古典概型几何概型统计定义计算概率常用的方法定义法性质公式法模拟试验法公式法性质法几何定义法统计定义法古典定义法范围性总和性物理机械法计算机(软件)法乘法公式加法公式和积互补公式对偶律概率常用的求法(一)、定义法:3.几何定义法:1.统计定义法:4.公理化定义法:2.古典定义法:频率是概率的估计;频率的稳定值是概率有待大学提高补充之①基本思想:化归思想,化大为小①基本思想:数形结合思想,事件图形化②使用前提:①0有限性②0等可能性②使用前提:①0无限性②0等可能性参课本P:126参课本P:136估计稳定是概率古典概型个数比几何概型测度比有限无限是区分参课本P:110(一)、定义法:(三)、性质公式法:(二)、模拟试验法:3.几何定义法1.统计定义法4.公理化定义法2.古典定义法①范围性②乘法公式①加法公式③和积互补公式④对偶律②总和性2.公式法:1.性质法:1.物理机械法:2.计算机(软件)法:(三)、性质公式法:①范围性②总...