二项式定理展开式VIP免费

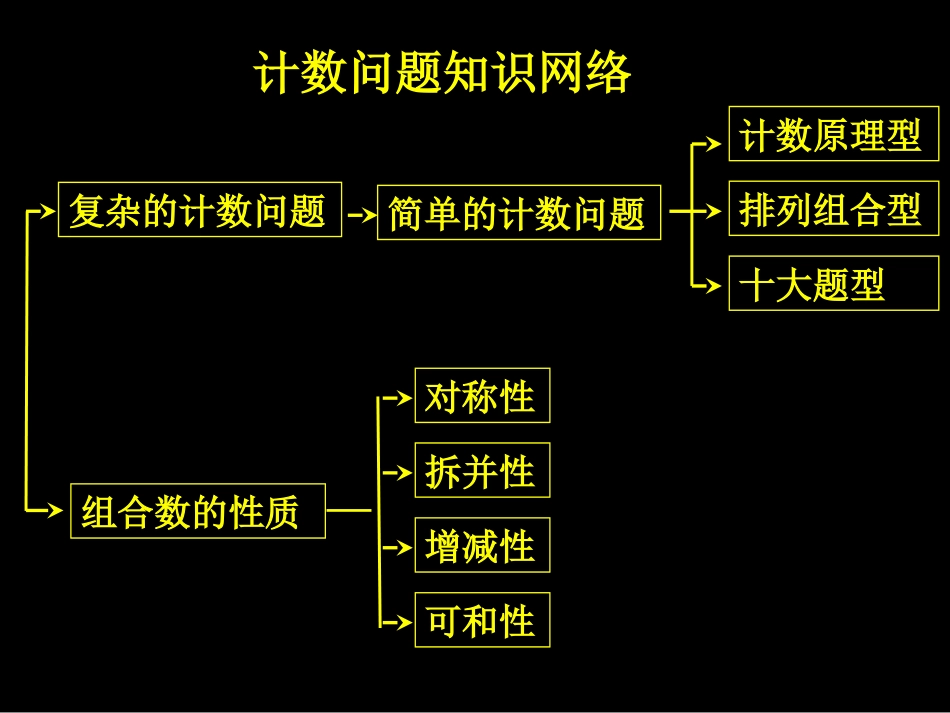
§247二项式定理——展开式一、杨辉三角形：三、二项式的展开式：二、二项式定理：2.通项公式：1.展开式：3.系数与二项式系数：nnnrrnrnnnnnnbCbaCbaCaCba110)(“前项后项+”相连展开共有n+1三块组成每一项前降后升和为nnnnrrnrnnnnnnCCCC110)(注2：nnnnnnnCCCC2210)1(注1：计数问题知识网络复杂的计数问题组合数的性质对称性简单的计数问题排列组合型拆并性增减性可和性计数原理型十大题型计数问题总述：两理两数四原则十大题型递推法⑤注①：分类加法及分步乘法计数原理：①②③④注④：注②：排列数与组合数：注⑤：设n元某计数问题共有an种方法若求an的通项公式有难度，可考虑求其递推公式化大为小是共性顾名思义是区分①相邻(捆绑法)○注③：①先理后数②先组后排③特殊优先④正难则反○○○○⑧错排○②不邻(插空法)○③在与不在④含与不含⑤至多与至少○○○直接法间接法⑥分组○相同元素不同元素⑦分配○均匀分配非均匀分配二元1种三元2种四元9种⑩染色○⑨定序○1.分类加法计数原理：2.分步乘法计数原理：完成一件事有n类方式,在第一类方式中有m1种不同的方法,在第二类方式中有m2种不同的方法……,在第n类方式中有mn种不同的方法.那么完成这件事共有N=m1+m2+…+mn种不同的方法完成一件事需要分成n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法……,做第n步有mn种不同的方法那么完成这件事共有N=m1×m2×…×mn种不同的方法先把包含于某内容中的所有对象的数目计算出来3.容斥计数原理:再把重复计算的数目排斥出去,这种计数的方法共同点不同点说明化大为小是共性顾名思义是区分都是采用“分”的手法，将大事件化为小事件“分类”是指完成事件共有n类办法每类办法都能独立地完成这件事类似于物理中的并联电路“分步”是指完成事件共有n个步骤类似于物理中的串联电路每一步都不能独立完成这件事最终结果“分类”用“加法”最终结果“分步”用“乘法”“分类”要不重不漏；各类间要互斥独立“分步”要连续完整；各步间要关联独立1.阶乘：2.排列数：3.组合数：nn321!)1()2()1()!(!mnnnnmnnmnAmnnmnCC!mAmn注1.一般的，乘积式用于计算，阶乘式用于证明注2.常用的排列数：10nAnAn1！nAnn注3.常用的组合数：10nCnCn11nnC两理两数四原则十大题型递推法排列与组合的关联：排列可以看作是先取组合，再做全排列先组后排：排列有序，组合无序，可用特值法来验证有无顺序①②两理两数四原则十大题型递推法①先理后数②先组后排③特殊优先④正难则反两理两数四原则十大题型递推法!mCAmnmn①相邻——捆绑法⑧错排：二元1种；三元2种；四元9种……②不邻(相离)——插空法⑥分组相同元素——0-1法不同元素——公式法⑩染色——递推法⑨定序——倍缩法(等概率法)；插空法两理两数四原则十大题型递推法③在与不在④含与不含⑤至多与至少特殊优先直接法正难则反间接法——⑦分配均匀分配非均匀分配先分组后分配1.相邻问题捆绑法：引：相间问题位置法2.不邻(相离)问题插空法：先捆可邻成大元次变个数全排列先排可邻后插空多元切忌间接法二元可用间接法亮灯空位是变式相邻相离综合体一般解法位置法3.在与不在4.含与不含5.至多与至少特殊优先直接法正难则反间接法——6.错排：①背诵法：a2=1；a3=2；a4=9；a5=44……②递推法：nnnnnnnnaCaCaCaCA221110))(1(21nnnaana①〇②〇9.分配：8.分组：(1)相同元素的分组：参分配(2)不同元素的非均匀分组：常规法处理(3)不同元素的均匀分组：(4)不同元素的混合分组：(1)不同元素的分配：(2)相同元素的分配(分组)：!22nnnnCC①将2n个不同元素均匀的分成2组,共有种分法②将3n个不同元素均匀的分成3组,共有种分法!323nnnnnnCCC先均匀后非均匀先分组后分配0—1法7.定序：①倍缩法(等概率法)：②插空法：!!mnNnmnNA10.染色问题：(1)条型域：如图，,用k种颜色染n块区域，相邻…32n11)1(nnkkt区域不能同色,则共有种染法注1：染色基础是条型方法多多随爱好...