离散型随机变量的方法VIP免费

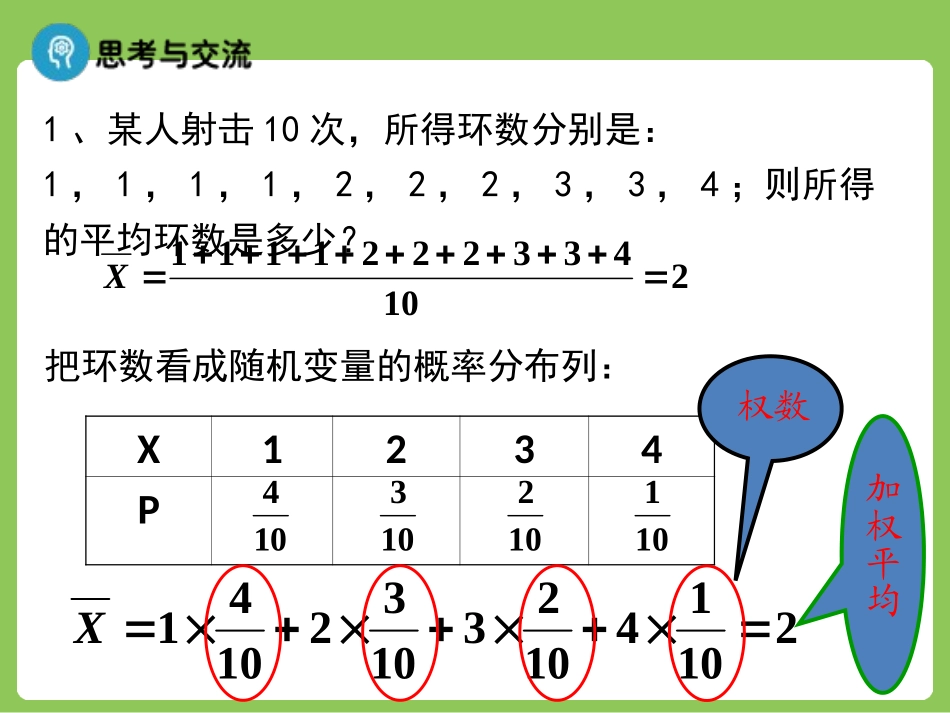
2.3.1离散型随机变量的均值人教A版选修2-3第二章对于离散型随机变量，可以由它的概率分布列确定与该随机变量相关事件的概率。但在实际问题中，有时我们更感兴趣的是随机变量的某些数字特征。例如，要了解某班同学在一次数学测验中的总体水平，很重要的是看平均分；要了解某班同学数学成绩是否“两极分化”则需要考察这个班数学成绩的方差。我们还常常希望直接通过数字来反映随机变量的某个方面的特征，最常用的有期望与方差.1、某人射击10次，所得环数分别是：1，1，1，1，2，2，2，3，3，4；则所得的平均环数是多少？2104332221111X把环数看成随机变量的概率分布列：X1234P10410310210121014102310321041X权数加权平均2、某商场要将单价分别为18元/kg，24元/kg，36元/kg的3种糖果按3：2：1的比例混合销售，如何对混合糖果定价才合理？X182436P把3种糖果的价格看成随机变量的概率分布列：636261)/(23613631242118kgX元一、离散型随机变量取值的平均值数学期望一般地，若离散型随机变量X的概率分布为：nniipxpxpxpxXE2211)(则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。P1xix2x······1p2pip······nxnpX设Y＝aX＋b，其中a，b为常数，则Y也是随机变量．（1）Y的分布列是什么？（2）E(Y)=？思考：P1xix2x······1p2pip······nxnpXnniipxpxpxpxXE2211)(P1xix2x······1p2pip······nxnpXP1xix2x······1p2pip······nxnpXYbax1baxibax2······baxnnnpbaxpbaxpbaxYE)()()()(2211)()(212211nnnpppbpxpxpxabXaE)(一、离散型随机变量取值的平均值数学期望1122()iinnEXxpxpxpxpP1xix2x······1p2pip······nxnpX二、数学期望的性质()()EaXbaEXb要点离散型随机变量均值的性质应用求均值的关键是求出分布列，只要求出随机变量的分布列，就可以套用均值的公式求解，对于aX＋b型随机变量的均值，可以利用均值的性质求解，当然也可以先求出aX＋b的分布列，再用定义求解．已知随机变量X的分布列如下：X－2－1012P141315m120(1)求m的值；(2)求E(X)；(3)若Y＝2X－3，求E(Y)．【思路启迪】解答本题可先由分布列的性质求出m的值，然后由随机变量的均值计算公式求出相应的期望值，而对于(3)可以直接利用公式E(Y)＝E(2X－3)＝2E(X)－3，也可以先写出Y的分布列，再求E(Y)．【解】(1)由随机变量分布列的性质，得14＋13＋15＋m＋120＝1，解得m＝16.(2)E(X)＝(－2)×14＋(－1)×13＋0×15＋1×16＋2×120＝－1730.(3)方法一：由公式E(aX＋b)＝aE(X)＋b，得E(Y)＝E(2X－3)＝2E(X)－3＝2×－1730－3＝－6215.方法二：由于Y＝2X－3，所以Y的分布列如下：Y－7－5－3－11P14131516120所以E(Y)＝(－7)×14＋(－5)×13＋(－3)×15＋(－1)×16＋1×120＝－6215.若给出的随机变量ξ与X的关系为ξ＝aX＋b，a，b为常数．一般思路是先求出E(X)，再利用公式E(aX＋b)＝aE(X)＋b求E(ξ)．也可以利用ξ的分布列得到η的分布列，关键由ξ的取值计算η的取值，对应的概率相等，再由定义法求得E(η)．1、随机变量ξ的分布列是ξ135P0.50.30.2(1)则E(ξ)=.2、随机变量ξ的分布列是2.4(2)若η=2ξ+1，则E(η)=.5.8ξ47910P0.3ab0.2E(ξ)=7.5,则a=b=.0.40.1例1.篮球运动员在比赛中每次罚球命中得1分，罚不中得0分．已知某运动员罚球命中的概率为0.7，则他罚球1次的得分X的均值是多少？一般地，如果随机变量X服从两点分布，X10Pp1－p则pppEX)1(01小结：与两点分布、二项分布有关的均值例2.篮球运动员在比赛中每次罚球命中得1分，罚不中得0分．已知某运动员罚球命中的概率为0.7，他连续罚球3次；（1）求他得到的分数X的分布列；（2）求X的期望。X0123P33.0解：(1)X～B（3，0.7）2133.07.0C3.07.0223C37.0(2)31222333()00.310.70.320.70.330.7EXCC1.2)(XE7.03一般地，如果随机变量X服从二项分布，即X～B（n,p），则npX...